题目内容
 如图,一张正方形纸板的边长为10cm,将它割去一个正方形,留下四个全等的直角三角形(图中阴影部分).设AE=BF=CG=DH=x(cm),阴影部分的面积为y(cm2)
如图,一张正方形纸板的边长为10cm,将它割去一个正方形,留下四个全等的直角三角形(图中阴影部分).设AE=BF=CG=DH=x(cm),阴影部分的面积为y(cm2)(1)求y关于x的函数解析式和自变量x的取值范围;
(2)当x取何值时,阴影部分的面积达到最大,最大值为多少?
(3)当留下的四个直角三角形恰好能拼成一个正方形时(无缝无重叠),求此时x的值.
考点:二次函数的应用,一元二次方程的应用
专题:几何图形问题
分析:(1)利用直角三角形面积公式求出即可;
(2)利用配方法求出二次函数顶点式形式,得出x的值即可;
(3)利用正方形的性质得出两直角边的比,进而求出阴影部分面积.
(2)利用配方法求出二次函数顶点式形式,得出x的值即可;
(3)利用正方形的性质得出两直角边的比,进而求出阴影部分面积.
解答:解:(1)设AE=BF=CG=DH=x(cm),
阴影部分的面积为:y=4×
x(10-x)=-2x2+20x,(0<x<10);
(2)∵y=-2x2+20x=-2(x2-10x)=-2(x-5)2+50,
∴当x=5时,阴影部分的面积达到最大,最大值为50;
(3)当四个直角三角形刚好拼接成正方形时,
即两直角边的比为:1:2,
故x=2(10-x),
解得:x=
,
阴影部分的面积是:y=-2x2+20x=-2×(
)2+20×
=
.
阴影部分的面积为:y=4×
| 1 |
| 2 |
(2)∵y=-2x2+20x=-2(x2-10x)=-2(x-5)2+50,
∴当x=5时,阴影部分的面积达到最大,最大值为50;
(3)当四个直角三角形刚好拼接成正方形时,
即两直角边的比为:1:2,
故x=2(10-x),
解得:x=
| 10 |
| 3 |
阴影部分的面积是:y=-2x2+20x=-2×(
| 10 |
| 3 |
| 10 |
| 3 |
| 400 |
| 9 |
点评:此题主要考查了二次函数的应用,利用正方形性质得出y与x的函数关系是解题关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 实数a、b在数轴上的对应点如图所示,则下列不等式中错误的是( )
实数a、b在数轴上的对应点如图所示,则下列不等式中错误的是( )| A、a+b<0 | ||
| B、ab<0 | ||
| C、a-b<0 | ||
D、
|
下列各式中,正确的是( )
| A、a5÷a5=0 | ||
B、(2a)-1=
| ||
| C、(x3)4÷(-x2)3=-x2 | ||
| D、(x2-y2)2=x4-y4 |
 如图所示,在直角坐标系中,O(0,0),P(2,1),Q是坐标轴上的一点,若△OPQ成等腰三角形,则Q点所在的位置有( )
如图所示,在直角坐标系中,O(0,0),P(2,1),Q是坐标轴上的一点,若△OPQ成等腰三角形,则Q点所在的位置有( )| A、4处 | B、6处 | C、7处 | D、8处 |
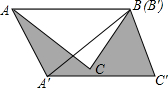 如图,在△ABC中,∠BAC=45°,AB=4cm,将△ABC绕点B按逆时针方向旋转45°后得到△A′BC′,则阴影部分的面积为
如图,在△ABC中,∠BAC=45°,AB=4cm,将△ABC绕点B按逆时针方向旋转45°后得到△A′BC′,则阴影部分的面积为 如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙C的距离为0.7米.
如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙C的距离为0.7米.