Question

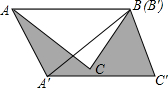如图，在△ABC中，∠BAC=45°，AB=4cm，将△ABC绕点B按逆时针方向旋转45°后得到△A′BC′，则阴影部分的面积为

 

．

Answer 1

考点：旋转的性质

专题：计算题

分析：AC与BA′相交于D，如图，根据旋转的性质得∠ABA′=45°，BA′BA=4，△ABC≌△A′BC′，则S_△ABC=S_△A′BC′，再利用面积的和差可得S_阴影部分=S_△ABA′，接着证明△ADB为等腰直角三角形，得到∠ADB=90°，AD=

2

2

AB=2

2

，然后利用三角形面积公式计算S_△ABA，从而得到S_阴影部分．

解答：解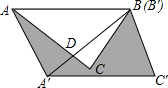：AC与BA′相交于D，如图，
∵△ABC绕点B按逆时针方向旋转45°后得到△A′BC′，
∴∠ABA′=45°，BA′BA=4，△ABC≌△A′BC′，
∴S_△ABC=S_△A′BC′，
∵S_{四边形AA′C′B}=S_△ABC+S_阴影部分=S_△A′BC′+S_△ABA′，
∴S_阴影部分=S_△ABA′，
∵∠BAC=45°，
∴△ADB为等腰直角三角形，
∴∠ADB=90°，AD=

2

2

AB=2

2

，
∴S_△ABA′=

1

2

AD•BA′=

1

2

×2

2

×4=4

2

（cm²），
∴S_阴影部分=4

2

cm²．
故答案为：4

2

cm²．

点评：本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了等腰直角三角形的性质．运用面积的和差解决不规则图形的面积是解决此题的关键．