Question

如图，一架2.5米长的梯子AB斜靠在竖直的墙AC上，这时B到墙C的距离为0.7米．
（1）如果梯子的顶端沿墙下滑0.4米，那么点B将向外移动多少米？
（2）如果梯子的顶端沿墙下滑0.9米，那么该题的答案会是0.9米吗？为什么？
（3）梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离，有可能相等吗？为什么？

Answer 1

考点：勾股定理的应用

专题：

分析：（1）在Rt△ABC中，根据已知条件运用勾股定理可将AC的长求出，又知AA₁的长可得AC的长，在Rt△A₁B₁C中再次运用勾股定理可将B₁C求出，B₁C的长减去BC的长即为底部B外移的距离．
（2）作法与（1）相同；
（3）设梯子顶端从A处下滑x米，点B向外也移动x米，根据勾股定理可得（x+0.7）²+（2.4-x）²=2.5²，再解即可．

解答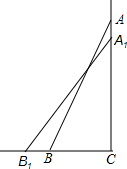：解：（1）在Rt△ABC中，∵AB=2.5，BC=0.7，
∴AC=

AB2-CB2

=

2．52-0．72

=2.4米，
又∵AA₁=0.4，
∴A₁C=2.4-0.4=2，
在Rt△A₁B₁C中，B₁C=

2．52-22

=1.5米，
则BB₁=CB₁-CB=1.5-0.7=0.8米．
故：梯子底部B外移0.8米．

（2）不会是0.9米；
∵AA₁=0.9，
∴A₁C=2.4-0.9=1.5，
在Rt△A₁B₁C中，B₁C=

2．52-1．52

=2米，
则BB₁=CB₁-CB=2-0.7=1.3米．
故：梯子底部B外移1.3米．

（3）有可能．
设梯子顶端从A处下滑x米，点B向外也移动x米，
则有（x+0.7）²+（2.4-x）²=2.5²，
解得：x₁=1.7或x₂=0（舍）
故当梯子顶端从A处下滑1.7米时，点B向外也移动1.7米，即梯子顶端从A处沿墙AC下滑的距离与点B向外移动的距离有可能相等．

点评：本题主要考查了勾股定理的应用及一元二次方程的应用，根据题意得出关于x的一元二次方程是解答此题的关键．