题目内容
4.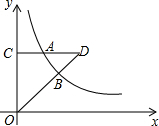 如图,A,B是反比例函数y=$\frac{k}{x}$(k>0,x>0)图象上两点,AC⊥y轴于C,CA交OB于D,已知$\frac{BD}{OB}$=$\frac{1}{2}$,S四边形OBAC=11,则k=12.
如图,A,B是反比例函数y=$\frac{k}{x}$(k>0,x>0)图象上两点,AC⊥y轴于C,CA交OB于D,已知$\frac{BD}{OB}$=$\frac{1}{2}$,S四边形OBAC=11,则k=12.
分析 过点B作BE⊥x轴于E,过点D作DF⊥x轴于F,连接AO,设B(a,b),结果k的几何意义得到S△OAC=S△OBE=$\frac{ab}{2}$=$\frac{k}{2}$,再根据图形面积之间的关系列方程求解.
解答  解:过点B作BE⊥x轴于E,过点D作DF⊥x轴于F,连接AO,
解:过点B作BE⊥x轴于E,过点D作DF⊥x轴于F,连接AO,
设B(a,b),
∵$\frac{BD}{OB}$=$\frac{1}{2}$,∴D($\frac{3a}{2}$,$\frac{3b}{2}$),
∵A,B都在反比例函数y=$\frac{k}{x}$(k>0,x>0)图象上,
∴S△OAC=S△OBE=$\frac{ab}{2}$=$\frac{k}{2}$,
∵S四边形OBAC=11,
∴S△AOB=11-$\frac{ab}{2}$,
∴S△AOD=$\frac{3}{2}$(11-$\frac{ab}{2}$),
∵S△CDO=S△ODF,
∴S四边形BEFD=S△AOD,
∴$\frac{3}{2}$(11-$\frac{ab}{2}$)=(b+$\frac{3b}{2}$)(a-$\frac{3a}{2}$),
∴ab=12,
即:k=12,
故答案为:12.
点评 本题考查了反比例函数系数k的几何意义,平行线分线段成比例,三角形的面积公式的应用,解答此题的关键是根据反比例函数系数k的几何意义求出k的值,

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.下列命题不正确的是( )
| A. | 相等的角是对顶角 | |
| B. | 平移前后图形的形状和大小都没有发生改变 | |
| C. | 两条平行线被第三条直线所截,同旁内角互补 | |
| D. | 在同一平面内,过直线外一点有且只有一条直线与该直线平行 |
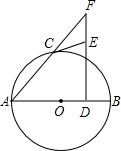 如图,AB是⊙O的直径,C是⊙O上一点,D是OB中点,过点D作AB的垂线交AC的延长线于点F.过点C作⊙O的切线交FD于点E.
如图,AB是⊙O的直径,C是⊙O上一点,D是OB中点,过点D作AB的垂线交AC的延长线于点F.过点C作⊙O的切线交FD于点E. 如图,小明用自制的直角三角形纸板DEF测量树AB的高度,测量时,使直角边DF保持水平状态,其延长线交AB于点G;使斜边DE所在的直线经过点A.测得边DF离地面的高度为1m,点D到AB的距离等于7.5m.已知DF=1.5m,EF=0.6m,那么树AB的高度等于( )
如图,小明用自制的直角三角形纸板DEF测量树AB的高度,测量时,使直角边DF保持水平状态,其延长线交AB于点G;使斜边DE所在的直线经过点A.测得边DF离地面的高度为1m,点D到AB的距离等于7.5m.已知DF=1.5m,EF=0.6m,那么树AB的高度等于( ) 如图,∠AOB=90°,C、D是$\widehat{AB}$的三等分点,AB分别交OC、OD于点E、F,求证:AE=CD.
如图,∠AOB=90°,C、D是$\widehat{AB}$的三等分点,AB分别交OC、OD于点E、F,求证:AE=CD.