题目内容
9.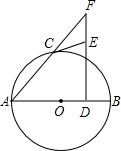 如图,AB是⊙O的直径,C是⊙O上一点,D是OB中点,过点D作AB的垂线交AC的延长线于点F.过点C作⊙O的切线交FD于点E.
如图,AB是⊙O的直径,C是⊙O上一点,D是OB中点,过点D作AB的垂线交AC的延长线于点F.过点C作⊙O的切线交FD于点E.(1)求证:CE=EF;
(2)如果sinF=$\frac{3}{5}$,EF=$\frac{5}{2}$,求AB的长.
分析 (1)连结OC,由CE为⊙O的切线,得到OC⊥CE,又因为FD⊥AB,推出∠3=∠F,得到结论CE=EF;
(2)根据三角函数,设出AD=3k,AF=5k,可得FD=4k,连结CB交FD于点G,由AB为⊙O直径,得到∠ACB=∠FCB=90°,推出∠F=∠B,再根据边角关系得出结论.
解答 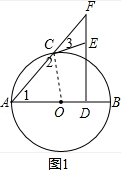 (1)证明:如图1,连结OC,
(1)证明:如图1,连结OC,
∵CE为⊙O的切线,
∴OC⊥CE,
∴∠OCE=90°,
∴∠2+∠3=90°,
∵FD⊥AB,∴∠F+∠1=90°,
又∵OC=OA,∴∠1=∠2,
∴∠3=∠F,
∴CE=EF;
(2)解:如图2∵FD⊥AB,sin∠F=$\frac{3}{5}$,
设AD=3k,AF=5k,可得FD=4k,
∵D为OB中点∴DB=k,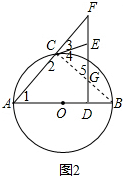
连结CB交FD于点G,
∵AB为⊙O直径,∴∠ACB=∠FCB=90°,
∴∠F=∠B,
∵DB=k,
∴GD=$\frac{3}{4}$k,可得FG=$\frac{13}{4}$k,
∵∠FCB=90°,∴∠5+∠F=∠3+∠4,
∵∠F=∠3,∴∠4=∠5,
∴CE=EF=EG,
∵EF=$\frac{5}{2}$,∴FG=5,
∴$\frac{13k}{4}$=5,∴k=$\frac{20}{13}$,
∴AB=$\frac{80}{13}$.
点评 本题考查了切线的性质,圆周角定理,等腰三角形的判定与性质,解题的关键是正确的作出辅助线.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
20.如果向东走5米记+5m,那么向西走3米记作( )
| A. | -2m | B. | -3m | C. | 2m | D. | 3m |
1.若二次函数y=ax2+bx+c(a≠0)与x轴交于两个不同点A(x1,0),B(x2,0);且二次函数化为顶点式是y=a(x-h)2+k,则下列说法:
①b2-4ac>0;
②x1+x2=2h;
③二次函数y=ax2+bx+2c(a≠0)化为顶点式为y=a(x-h)2+2k;
④若c=k,则一定有h=b.
正确的有( )
①b2-4ac>0;
②x1+x2=2h;
③二次函数y=ax2+bx+2c(a≠0)化为顶点式为y=a(x-h)2+2k;
④若c=k,则一定有h=b.
正确的有( )
| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
18.由若干个相同的小立方体搭成的几何体的三视图如图所示,则组成该几何体的小立方体有( )


| A. | 3块 | B. | 4块 | C. | 5块 | D. | 6块 |
 已知等腰直角△AOB,△CBD,双曲线y=$\frac{k}{x}$经过二个直角顶点A,C,D(6,0),求k.
已知等腰直角△AOB,△CBD,双曲线y=$\frac{k}{x}$经过二个直角顶点A,C,D(6,0),求k.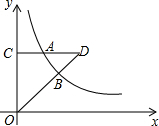 如图,A,B是反比例函数y=$\frac{k}{x}$(k>0,x>0)图象上两点,AC⊥y轴于C,CA交OB于D,已知$\frac{BD}{OB}$=$\frac{1}{2}$,S四边形OBAC=11,则k=12.
如图,A,B是反比例函数y=$\frac{k}{x}$(k>0,x>0)图象上两点,AC⊥y轴于C,CA交OB于D,已知$\frac{BD}{OB}$=$\frac{1}{2}$,S四边形OBAC=11,则k=12.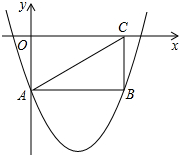 如图,矩形OABC的两边在坐标轴上,连接AC,抛物线y=x2-4x-2经过A,B两点.
如图,矩形OABC的两边在坐标轴上,连接AC,抛物线y=x2-4x-2经过A,B两点.