题目内容
5.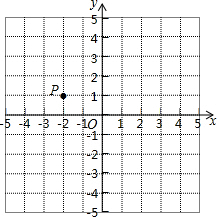 已知P(-2,1).(第(1)(2)要求保留必要的作图轨迹和简单的说理)
已知P(-2,1).(第(1)(2)要求保留必要的作图轨迹和简单的说理) (1)作出点P绕点O逆时针旋转90°的点P1并直接写出P1的坐标.
(2)作出点P关于原点的对称点的点P2,并求出PP2的长.
(3)若以PP2为直径作圆,直接写出在圆上的点(不同于P、P2的格点)的坐标(写出两个即可).
分析 (1)把点旋转的问题转化为线段旋转的问题,这样可确定P1点的位置,再写出P1的坐标;
(2)利用中心对称的性质,延长P1O到P2,使OP2=OP1,即可得到点P2,然后利用勾股定理计算PP2的长;
(3)以PP2为直径作圆,然后写出两个圆上格点的坐标即可.
解答 解:(1)如图,连结OP,把OP绕点O逆时针旋转90°得到OP1,则点P1为所作,P1的坐标为(-1,-2);
(2)如图,延长P1O到P2,使OP2=OP1,则点P2为所作,
PP2=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$;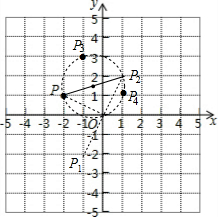
(3)点P3(-1,3),P4(1,2)在以PP2为直径的圆上.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了点与圆的位置关系.

练习册系列答案
相关题目
15.下列是无理数的是( )
| A. | 0.666… | B. | $\frac{22}{7}$ | C. | $\frac{π}{2}$ | D. | 2.626 266 62 |
 如图,∠1=∠2,∠3=∠4,EF⊥AD于F,求证:∠AEF=∠DEF.
如图,∠1=∠2,∠3=∠4,EF⊥AD于F,求证:∠AEF=∠DEF.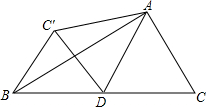 如图△ABC中,AD为底边上的中线,∠ADC=60°,BC=4,将△ADC沿AD翻折与△ADC′重合,则BC′=2.
如图△ABC中,AD为底边上的中线,∠ADC=60°,BC=4,将△ADC沿AD翻折与△ADC′重合,则BC′=2.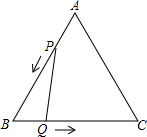 如图,已知△ABC是边长为3cm的等边三角形,动点P,Q同时从A,B两点出发,分别沿AB,BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P,Q两点都停止运动,设点P的运动时间为t(s).解答下列问题:
如图,已知△ABC是边长为3cm的等边三角形,动点P,Q同时从A,B两点出发,分别沿AB,BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P,Q两点都停止运动,设点P的运动时间为t(s).解答下列问题: