题目内容
19.有五个编号分别是Ⅰ、Ⅱ、Ⅲ、Ⅳ和Ⅴ的长方形,大小如表:| 长方形 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ |
| 长度 | 5 | 4 | 3 | 2 | 1 |
| 宽度 | x | x+1 | x+2 | x+3 | x+4 |
(2)通过计算,说明长方形Ⅳ、Ⅴ的面积不可能最大.
分析 (1)利用长方形的周长计算公式列式得出答案即可;
(2)利用作差法求得答案即可.
解答 解:(1)2(5+x)=10+2x;
2(4+x+1)=10+2x;
2(3+x+2)=10+2x;
2(2+x+3)=10+2x;
2(1+x+4)=10+2x;
所以五个长方形的周长相等;
(2)SⅠ=5x,
SⅡ=4x+4,
SⅢ=3x+6,
SⅣ=2x+6,
SⅤ=x+4,
SⅢ-SⅣ=3x+6-2x-6=x,SⅡ-SⅤ=4x+4-x-4=3x,
而x>0,
SⅢ>SⅣ,SⅡ>SⅤ,
所以长方形Ⅳ、Ⅴ的面积不可能最大.
点评 此题考查列代数式,掌握长方形的周长计算方法是解决问题的关键.

练习册系列答案
相关题目
9.对二次三项式x2-4x+3分解因式,结果为( )
| A. | x(x-4)+3 | B. | (x-1)(x-3) | C. | (x-1)(x+3) | D. | (x+1)(x-3) |
4.若数轴上的点M对应的数是-2$\frac{2}{3}$,那么与M相距1个单位长度的点N对应的数是( )
| A. | -1$\frac{1}{3}$ | B. | -3$\frac{2}{3}$ | C. | -3$\frac{2}{3}$与-1$\frac{2}{3}$ | D. | -3$\frac{2}{3}$与-1$\frac{1}{3}$ |
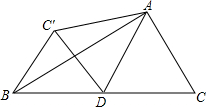 如图△ABC中,AD为底边上的中线,∠ADC=60°,BC=4,将△ADC沿AD翻折与△ADC′重合,则BC′=2.
如图△ABC中,AD为底边上的中线,∠ADC=60°,BC=4,将△ADC沿AD翻折与△ADC′重合,则BC′=2.