Question

如图，在Rt△ABC中，∠ABC=90°，AC=10，BC=6，∠ACB的平分线CO交AB于点O，以OB为半径作⊙O．
（1）请判断AC与⊙O的位置关系，并说明理由；
（2）求⊙O的半径．

Answer 1

考点：切线的判定

专题：

分析：（1）过点O作OD⊥AC于点D，根据角平分线性质得出OD=OB，根据切线的判定推出即可；
（2）根据勾股定理求出AB，证△AOD∽△ACB，得出比例式，代入求出即可．

解答：解：（1）AC=⊙O相切，
理由如下：过点O作OD⊥AC于点D，
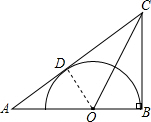
∵∠ABC=90°，
∴OB⊥CB，
又∵OC平分∠ACB，
∴OD=OB，
∴AC与⊙O相切；

（2）∵在Rt△ABC中，AC=10，BC=6，
∴AB=

AC2-BC2

=8，
∵OD⊥AC，
∴∠ODA=∠B=90°
又∵∠A=∠A，
∴△AOD∽△ACB，
∴

OD

CB

=

AO

AC

，
设⊙O的半径为x，
∴

x

6

=

8-x

10

，
解得：x=3，
即⊙O的半径为3．

点评：本题考查了切线的判定和勾股定理，也考查了相似三角形的性质和判定，还考查了角平分线性质，综合运用性质进行推理和计算是解此题的关键．