题目内容
5.已知二次函数y=x2+kx-6的图象向右平移3个单位后恰好经过原点,则k的值为$\frac{2}{3}$.分析 先利用配方法得到二次函数y=x2+kx-6的图象的顶点坐标为(-$\frac{k}{2}$,-6-$\frac{{k}^{2}}{4}$),再根据点平移的规律得到点(-$\frac{k}{2}$,-6-$\frac{{k}^{2}}{4}$)经过平移后所得对应点的坐标为(-$\frac{k}{2}$+3,-6-$\frac{{k}^{2}}{4}$),然后根据顶点式写出平移后的二次函数图象的解析式.
解答 解:∵y=x2+kx-6=(x+$\frac{k}{2}$)2-6-$\frac{{k}^{2}}{4}$,
∴该抛物线的顶点坐标是(-$\frac{k}{2}$,-6-$\frac{{k}^{2}}{4}$),向右平移3个单位后所得对应点的坐标为(-$\frac{k}{2}$+3,-6-$\frac{{k}^{2}}{4}$),
∴平移后的二次函数图象的解析式是y=(x+$\frac{k}{2}$-3)2-6-$\frac{{k}^{2}}{4}$,
把(0,0)代入,得
0=(0+$\frac{k}{2}$-3)2-6-$\frac{{k}^{2}}{4}$,
解得k=$\frac{2}{3}$.
故答案是:$\frac{2}{3}$.
点评 本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.将正整数依次按表规律排成四列,则根据表中的排列规律,数2016应排的位置是第672行第2列.
| 第1列 | 第2列 | 第3列 | 第4列 | |
| 第1行 | 1 | 2 | 3 | |
| 第2行 | 6 | 5 | 4 | |
| 第3行 | 7 | 8 | 9 | |
| 第4行 | 12 | 11 | 10 | |
| … |
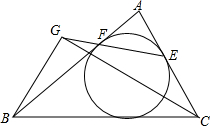 如图,△ABC的内切圆在AB、AC边上的切点分别为F、E,∠C的平分线交直线EF于G,求证:BG⊥CG.
如图,△ABC的内切圆在AB、AC边上的切点分别为F、E,∠C的平分线交直线EF于G,求证:BG⊥CG.