题目内容
20.不改变分式的值,使下列各分式的分子、分母中含x的最高次项的系数都是正数.(1)$\frac{4-x}{{x}^{2}-1}$;(2)$\frac{x+2}{-3+x-{x}^{2}}$;(3)$\frac{-{x}^{2}-1}{2-x}$.
分析 (1)根据分式的性质,可得答案.
(2)根据分式的性质,可得答案.
(3)根据分式的性质,可得答案.
解答 解:(1)$\frac{4-x}{{x}^{2}-1}$=-$\frac{x-4}{{x}^{2}-1}$;
(2)$\frac{x+2}{-3+x-{x}^{2}}$=-$\frac{x+2}{{x}^{2}}$-x+3;
(3)$\frac{-{x}^{2}-1}{2-x}$=$\frac{{x}^{2}+1}{x-2}$.
点评 本题考查了分式的性质,分式,分子、分母任意改变两项的符号,分式的值不变.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
10.如果x是最大的负整数,y绝对值最小的整数,则-x2016+y的值是( )
| A. | -2000 | B. | -1 | C. | 1 | D. | 2016 |
15.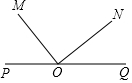 如图所示,在一条直线上顺次有P、O、Q三点,自O点在这条直线的同侧引两条射线OM、ON,如果∠MON=90°(∠POM为锐角),那么∠POM的余角是( )
如图所示,在一条直线上顺次有P、O、Q三点,自O点在这条直线的同侧引两条射线OM、ON,如果∠MON=90°(∠POM为锐角),那么∠POM的余角是( )
 如图所示,在一条直线上顺次有P、O、Q三点,自O点在这条直线的同侧引两条射线OM、ON,如果∠MON=90°(∠POM为锐角),那么∠POM的余角是( )
如图所示,在一条直线上顺次有P、O、Q三点,自O点在这条直线的同侧引两条射线OM、ON,如果∠MON=90°(∠POM为锐角),那么∠POM的余角是( )| A. | ∠MOQ | B. | ∠MON | C. | ∠NOQ | D. | ∠PON |
4.根据钟表就能知道具体时间了,那么时针1小时转过的角度是( )
| A. | 180° | B. | 90° | C. | 60° | D. | 30° |
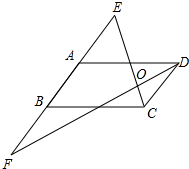 如图,平行四边形ABCD中,AB=2AD,AB=AE=BF,求证:EC⊥FD.
如图,平行四边形ABCD中,AB=2AD,AB=AE=BF,求证:EC⊥FD.
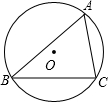 如图,△ABC内接于⊙O,已知AB=c,BC=a,AC=b,⊙O的半径为R.
如图,△ABC内接于⊙O,已知AB=c,BC=a,AC=b,⊙O的半径为R.