题目内容
17.已知关于x的一元二次方程x2-(2k+1)x+k(k+1)=0.(1)求证:方程必有两个不相等的实数根;
(2)k取何值时,方程有一个正根和一个负根.
分析 (1)求出△的值,再根据根的判别式判断即可;
(2)根据已知得出$\frac{c}{a}$<0,代入求出即可.
解答 (1)证明:∵△=[-(2k+1)]2-4(k2+1)=1>0,
∴方程必有两个不相等的实数根;
(2)解:设方程的两个根为e、f,
则ef=k(k+1),
当k(k+1)<0时,方程有一个正根和一个负根,
即-1<k<0时,方程有一个正根和一个负根.
点评 本题考查了根的判别式和根与系数关系的应用,能理解知识点是解此题的关键,注意:要知道一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.

练习册系列答案
相关题目
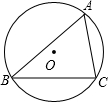 如图,△ABC内接于⊙O,已知AB=c,BC=a,AC=b,⊙O的半径为R.
如图,△ABC内接于⊙O,已知AB=c,BC=a,AC=b,⊙O的半径为R. 如图,王力的家在高楼15层,一天他去买竹竿,如果电梯的长、宽、高分别为1.2m,1.2m,2.3m,则他所买的竹竿最大长度是多少?
如图,王力的家在高楼15层,一天他去买竹竿,如果电梯的长、宽、高分别为1.2m,1.2m,2.3m,则他所买的竹竿最大长度是多少?