题目内容
16.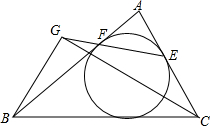 如图,△ABC的内切圆在AB、AC边上的切点分别为F、E,∠C的平分线交直线EF于G,求证:BG⊥CG.
如图,△ABC的内切圆在AB、AC边上的切点分别为F、E,∠C的平分线交直线EF于G,求证:BG⊥CG.
分析 如图,设AB与CG交于点K,内切圆的圆心为O,连接OA、OF、OB,想办法证明∠4=∠5,推出△GKF∽△BKO,推出$\frac{GK}{BK}$=$\frac{FK}{KO}$,即$\frac{GK}{FK}$=$\frac{BK}{KO}$,又∠BKG=∠OKF,推出△BKG∽△OKF,即可解决问题.
解答 证明:如图,设AB与CG交于点K,内切圆的圆心为O,连接OA、OF、OB.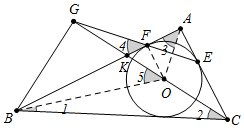
∵O是内心,
∴2∠1+2∠2+2∠3=180°,
∴∠1+∠2+∠3=90°,
∵E、F是切点,
∴∠AFO=∠OFK=90°,AO⊥EF,
∴∠3+∠AOF=90°,
∴∠AOF=∠1+∠2,
∵∠3+∠AFE=90°,∠3+∠AOF=90°,
∴∠4=∠AFE=∠AOF=∠1+∠2,
∵∠5=∠1+∠2,
∴∠4=∠5,
∵∠GKF=∠BKO,
∴△GKF∽△BKO,
∴$\frac{GK}{BK}$=$\frac{FK}{KO}$,
∴$\frac{GK}{FK}$=$\frac{BK}{KO}$,
∵∠BKG=∠OKF,
∴△BKG∽△OKF,
∴∠BGK=∠KFO=90°,
∴CG⊥BG.
点评 本题考查三角形内切圆与内心、相似三角形的判定和性质、切线长定理、切线的性质等知识,解题的关键是灵活应用所学知识,学会添加常用辅助线,构造相似三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目

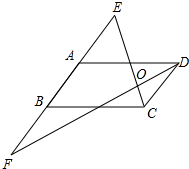 如图,平行四边形ABCD中,AB=2AD,AB=AE=BF,求证:EC⊥FD.
如图,平行四边形ABCD中,AB=2AD,AB=AE=BF,求证:EC⊥FD.