题目内容
20.为了解“阳光体育”活动情况,我市教育部门在某中学2000名学生中,随机抽取了若干学生进行问卷调查(要求每位学生只能填写一种自己喜欢的活动),并将调查的结果绘制成如图的两幅不完整的统计图:
根据以上信息解答下列问题:
(1)参加调查的人数共有300人;在扇形图中,表示“C”的扇形的圆心角为108度;
(2)补全条形统计图,并计算扇形统计图中的m;
(3)估计该校有多少名学生喜欢篮球?
分析 (1)用喜欢乒乓球的人数除以其所占的百分比可求得调查的总人数;用调查的总人数减去其余四个组的人数得到“C”的人数,用“C”的人数除以总人数再乘以360°得到表示“C”的扇形的圆心角的度数;
(2)用喜欢C项目的人数除以总人数即可求得其百分率,从而得到m的值;
(3)先求出喜欢篮球的学生所占的百分比即可得出该校喜欢篮球的学生人数.
解答 解:(1)观察统计图知喜欢乒乓球的有69人,占总人数的23%,
故调查的总人数有69÷23%=300人,
喜欢跳绳的有300-60-69-36-45=90人,
故C所表示的扇形的圆心角为$\frac{90}{300}$×360°=108°;
(2)m%=$\frac{60}{300}$×100%=20%,故m=20.
条形统计图补充如下;
(3)喜欢“篮球”的学生共有:
2000×$\frac{45}{300}$=300(名).
即该校有300名学生喜欢篮球.
故答案为300,108.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.也考查了用样本估计总体的思想.

练习册系列答案
相关题目
10.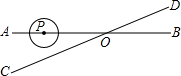 如图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在射线OA上,且与点O的距离为6cm,如果⊙P以1cm/s的速度沿由A向B的方向移动,那么⊙P与直线CD相切时运动时间为( )
如图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在射线OA上,且与点O的距离为6cm,如果⊙P以1cm/s的速度沿由A向B的方向移动,那么⊙P与直线CD相切时运动时间为( )
 如图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在射线OA上,且与点O的距离为6cm,如果⊙P以1cm/s的速度沿由A向B的方向移动,那么⊙P与直线CD相切时运动时间为( )
如图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在射线OA上,且与点O的距离为6cm,如果⊙P以1cm/s的速度沿由A向B的方向移动,那么⊙P与直线CD相切时运动时间为( )| A. | 4秒 | B. | 8秒 | C. | 4秒或6秒 | D. | 4秒或8秒 |
15.湿地观鸟、草莓采摘、海边烧烤是我市的特色旅游项目,今年“五一”期间我市共接待海内外游客24.1万人次,将24.1万用科学记数法可表示为( )
| A. | 2.41×106 | B. | 24.1×104 | C. | 2.41×104 | D. | 2.41×105 |
12.计算:a-2(1-3a)的结果为( )
| A. | 7a-2 | B. | -2-5a | C. | 4a-2 | D. | 2a-2 |
 如图,正方形ABCD的正方形CEFG的面积分别是7和5.
如图,正方形ABCD的正方形CEFG的面积分别是7和5.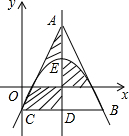 如图,点E是抛物线y=a(x-2)2+k的顶点,抛物线与y轴交于点C,过点C作CD∥x轴,与抛物线交于点B,与对称轴交于点D.点A是对称轴上一点,连结AC、AB.若△ABC是等边三角形,则图中阴影部分图形的面积之和是2$\sqrt{3}$.
如图,点E是抛物线y=a(x-2)2+k的顶点,抛物线与y轴交于点C,过点C作CD∥x轴,与抛物线交于点B,与对称轴交于点D.点A是对称轴上一点,连结AC、AB.若△ABC是等边三角形,则图中阴影部分图形的面积之和是2$\sqrt{3}$. 把一个含有45°角的三角板放在如图所示的两平行线上,测得∠α=120°,则∠β的度数为75°.
把一个含有45°角的三角板放在如图所示的两平行线上,测得∠α=120°,则∠β的度数为75°.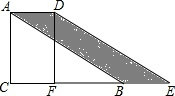 如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AB=8,将△ABC沿CB向右平移得到△DEF.若四边形ABED的面积等于8,则平移距离等于( )
如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AB=8,将△ABC沿CB向右平移得到△DEF.若四边形ABED的面积等于8,则平移距离等于( )