题目内容
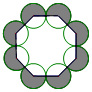
8. 如图矩形ABCD是一张标准纸,长BC=AD=$\sqrt{2}$,AB=CD=1,把△BCF沿CF对折使点B恰好落在边AD上的点E处,再把△DCH沿CH对折使点D落在线段CE上的点G处.
如图矩形ABCD是一张标准纸,长BC=AD=$\sqrt{2}$,AB=CD=1,把△BCF沿CF对折使点B恰好落在边AD上的点E处,再把△DCH沿CH对折使点D落在线段CE上的点G处.(1)求证:△AEF≌△GHE;
(2)利用该图形试求tan22.5°的值.
分析 根据折叠的性质得到CE=CB=$\sqrt{2}$,CG=CD=1,∠FEC=∠B=90°,∠HGC=∠HGE=∠D=90°,求得CE=$\sqrt{2}$CD,∠HGE=∠A=90°,根据三角函数的定义得到△EC是等腰直角三角形,得到AE=EG,根据全等三角形的判定定理即可得到结论;
(2)根据等腰直角三角形的性质得到EG=HG=DH=$\sqrt{2}$-1,根据三角函数的定义即可得到结论.
解答 解:(1)∵BC=AD=$\sqrt{2}$,AB=CD=1,
∵把△BCF沿CF对折使点B恰好落在边AD上的点E处,再把△DCH沿CH对折使点D落在线段CE上的点G处,
∴CE=CB=$\sqrt{2}$,CG=CD=1,∠FEC=∠B=90°,∠HGC=∠HGE=∠D=90°,
∴CE=$\sqrt{2}$CD,∠HGE=∠A=90°,
∴tan∠DEC=$\frac{CD}{EC}=\frac{\sqrt{2}}{2}$,EG=EC-GC=$\sqrt{2}$-1,
∴∠DEC=45°,
∴△DEC是等腰直角三角形,
∴∠AEF=45°,
∴DE=DC,∠AEF=∠DEC,
∴AE=AD-DE=$\sqrt{2}$-1,
∴AE=EG,
在△AEF与△GHE中,$\left\{\begin{array}{l}{∠A=∠EGH}\\{AE=EG}\\{∠AEF=∠GEH}\end{array}\right.$,
∴△AEF≌△GHE;
(2)由(1)知∠DCH=∠GCH=$\frac{1}{2}×$45°=2.5°,DH=GH,△HEG是等腰直角三角形,
∴EG=HG=DH=$\sqrt{2}$-1,
∴tan∠DCH=tan22.5°=$\frac{DH}{CD}$=$\sqrt{2}$-1.
点评 本题考查了翻折变换(折叠问题),全等三角形的判定和性质,等腰直角三角形的判定和性质,三角函数的定义,熟练掌握折叠的性质是解题的关键.

| A. | x≥-2且x≠0 | B. | x>0 | C. | -2≤x<0 | D. | 0<x≤2 |
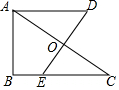
 如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1,正八边形外侧八个扇形(有阴影部分)面积之和为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )
如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1,正八边形外侧八个扇形(有阴影部分)面积之和为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | 1 |
 如图,Rt△ABC,∠B=90°,AC的垂直平分线交BC于点E,垂足为点O,过点A作BC的平行线,与直线OE交于点D,若AB=4,BC=6,则AD的长为$\frac{13}{3}$.
如图,Rt△ABC,∠B=90°,AC的垂直平分线交BC于点E,垂足为点O,过点A作BC的平行线,与直线OE交于点D,若AB=4,BC=6,则AD的长为$\frac{13}{3}$.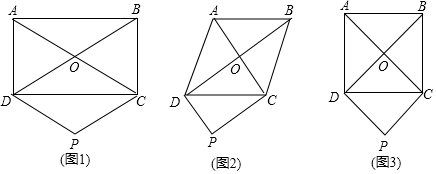
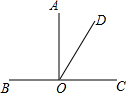 如图,AO⊥BC,垂足为O,且∠COD-∠AOD=34°28′.求∠BOD的度数.
如图,AO⊥BC,垂足为O,且∠COD-∠AOD=34°28′.求∠BOD的度数.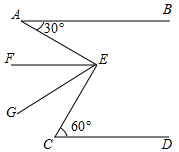 如图,AB∥CD,∠BAE=30°,∠ECD=60°,EF、EG等分∠AEC,试判断EF与AB的关系并写出你的理由.
如图,AB∥CD,∠BAE=30°,∠ECD=60°,EF、EG等分∠AEC,试判断EF与AB的关系并写出你的理由.