题目内容
6．
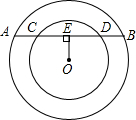已知：如图，在两个同心圆中，大圆的弦AB与小圆相交于点C、D，且AC=CD，DE⊥AB，垂足为点E，求证：BC=4ED．
分析 根据垂径定理得到AE=BE，CE=DE，得到AC=BD，等量代换得到CD=BD，于是得到结论．
解答 解：∵DE⊥AB，
∴AE=BE，CE=DE，
∴AC=BD，
∵AC=CD，
∴CD=BD，
∵CD=2DE，
∴BD=2DE，
∴BC=4ED．
点评 本题考查了直线与圆的位置关系，垂径定理，熟练掌握垂径定理是解题的关键．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
名师点睛字词句段篇系列答案
相关题目
如图，在等腰直角△ABC中，∠ACB=90°，AC=BC=$\sqrt{2}$
1．下列各式正确的是（ ）
| A． | ${x^6}•{x^{-2}}={x^{-12}}=\frac{1}{{{x^{12}}}}$ | B． | ${x^6}÷{x^{-2}}={x^{-3}}=\frac{1}{x^3}$ | ||
| C． | ${（x{y^{-2}}）^3}={x^3}{y^{-2}}=\frac{x^3}{y^2}$ | D． | ${（{\frac{y^3}{x^2}}）^{-1}}=\frac{x^2}{y^3}$ |
11．
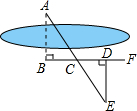如图，要测量河两岸相对的两点A、B的距离，先在AB的垂线BF上取两点C、D，使BC=CD，再作出BF的垂线DE，使点A、C、E在同一条直线上（如图所示），可以说明△ABC≌△EDC，得AB=DE，因此测得DE的长就是AB的长，判定△ABC≌△EDC，最恰当的理由是（ ）
如图，要测量河两岸相对的两点A、B的距离，先在AB的垂线BF上取两点C、D，使BC=CD，再作出BF的垂线DE，使点A、C、E在同一条直线上（如图所示），可以说明△ABC≌△EDC，得AB=DE，因此测得DE的长就是AB的长，判定△ABC≌△EDC，最恰当的理由是（ ）| A． | 边角边 | B． | 角边角 | C． | 边边边 | D． | 边边角 |
18．在下列长度的各组线段中，能组成直角三角形的是（ ）
| A． | 5，6，7 | B． | $\sqrt{2}$，$\sqrt{5}$，$\sqrt{7}$ | C． | 1，4，9 | D． | 5，11，12 |
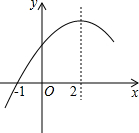二次函数y=ax2+bx+c（a≠0）的部分图象如图所示，图象过点（-1，0），对称轴为直线x=2，下列结论：（1）4a+b=0；（2）9a+c＞3b；（3）若点A（-3，y1）、点B（-$\frac{1}{2}$，y2）、点C（$\frac{7}{2}$，y3）在该函数图象上，则y1＜y3＜y2；（4）若方程a（x+1）（x-5）=-3的两根为x1和x2，且x1＜x2，则x1＜-1＜5＜x2．其中正确结论的序号是①④．