题目内容
15.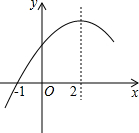 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)若点A(-3,y1)、点B(-$\frac{1}{2}$,y2)、点C($\frac{7}{2}$,y3)在该函数图象上,则y1<y3<y2;(4)若方程a(x+1)(x-5)=-3的两根为x1和x2,且x1<x2,则x1<-1<5<x2.其中正确结论的序号是①④.
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)若点A(-3,y1)、点B(-$\frac{1}{2}$,y2)、点C($\frac{7}{2}$,y3)在该函数图象上,则y1<y3<y2;(4)若方程a(x+1)(x-5)=-3的两根为x1和x2,且x1<x2,则x1<-1<5<x2.其中正确结论的序号是①④.
分析 由抛物线的对称轴方程得到b=-4a>0,则可对①进行判断;由于x=-3时,y<0,则可对②进行判断;
解答 解:∵抛物线的对称轴为直线x=-$\frac{b}{2a}$=2,
∴b=-4a>0,即4a+b=0,所以①正确;
∵x=-3时,y<0,
∴9a-3b+c<0,即9a+c<3b,所以②错误;
∵抛物线的对称轴为直线x=-$\frac{b}{2a}$=2,图象与x轴交于(-1,0),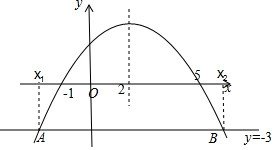
∴抛物线x轴的另一个交点是(5,0),
∵点A(-3,y1)、点B(-$\frac{1}{2}$,y2)、点C($\frac{7}{2}$,y3),
∵$\frac{7}{2}$-2=$\frac{3}{2}$,2-(-$\frac{1}{2}$)=$\frac{5}{2}$,
∴$\frac{3}{2}$<$\frac{5}{2}$
∴点C离对称轴的距离近,
∴y3>y2,
∵a<0,-3<-$\frac{1}{2}$<2,
∴y1<y2
∴y1<y2<y3,故(4)错误.
如图,∵a<0,
∴(x+1)(x-5)=-3/a>0,
即(x+1)(x-5)>0,
故x<-1或x>5,故(5)正确.
故答案为:①④.
点评 本题考查了二次函数图象与系数的关系:对于二次函数y=ax2+bx+c(a≠0),a决定抛物线的开口方向和大小,当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

| A. | 若a>b,则a+c>b+c | B. | 若a+c>b+c,则a>b | C. | 若a>b,则ac2>bc2 | D. | 若a>b,则1+a>b-1 |
| A. | -7°C | B. | 7°C | C. | -9°C | D. | 9°C |
| A. | 调查白银市市民的吸烟情况 | |
| B. | 调查白银市电视台某节目的收视率 | |
| C. | 调查白银市市民家庭日常生活支出情况 | |
| D. | 调查白银市某校八年级二班学生对“文明白银”的知晓率 |
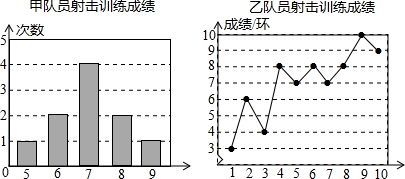
根据以上信息,整理分析数据如下:
| 平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
| 甲 | 7 | 7 | 7 | 1.2 |
| 乙 | 7 | 7.5 | 8 | 4.2 |
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
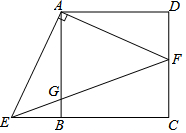 如图,在正方形ABCD中,F是CD边上的一点,AE⊥AF,AE交CB的延长线于点E,连接EF交AB于点G.
如图,在正方形ABCD中,F是CD边上的一点,AE⊥AF,AE交CB的延长线于点E,连接EF交AB于点G.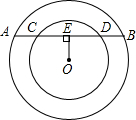 已知:如图,在两个同心圆中,大圆的弦AB与小圆相交于点C、D,且AC=CD,DE⊥AB,垂足为点E,求证:BC=4ED.
已知:如图,在两个同心圆中,大圆的弦AB与小圆相交于点C、D,且AC=CD,DE⊥AB,垂足为点E,求证:BC=4ED.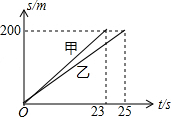 如图所示的是甲、乙两人在争夺冠军中的比赛图,其中t表示赛跑时所用时间,s表示赛跑的距离,根据图象回答下列问题:
如图所示的是甲、乙两人在争夺冠军中的比赛图,其中t表示赛跑时所用时间,s表示赛跑的距离,根据图象回答下列问题: 已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AE平分∠BAC的外角,DE∥AB交AE于点E.试说明四边形ADCE是矩形.
已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AE平分∠BAC的外角,DE∥AB交AE于点E.试说明四边形ADCE是矩形.