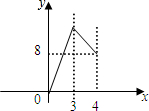题目内容
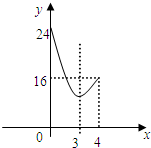
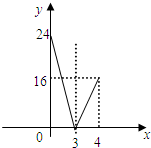
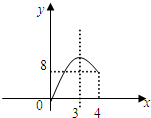
1.(1)如图①,在△ABC中,D为BC边上中点,则△ABD和△ADC的面积相等,那么在图②中,如果M、N分别为四边形ABCD的边AD、BC的中点,则图中四边形BNDM的面积S1和四边形ABCD面积S之间的关系是1:2;(2)如图③,在四边形ABCD中,M、N分别为AD、BC的中点,MB交AN于点P,MC交DN于Q,若四边形MPNQ的面积为36,求两个三角形ABP、DCQ的面积和.
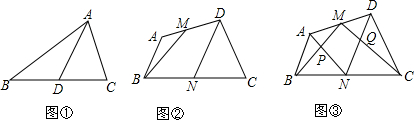
分析 (1)连结BD,根据等底等高的三角形的面积相等,可知三角形BDM的面积等于三角形ABM的面积,三角形CDN的面积等于三角形BDN的面积,据此解答;
(2)如图:连结BD,根据等底等高的三角形的面积相等进行解答即可.
解答 解:(1)如图②,连结BD,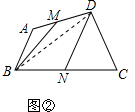
根据等底等高的三角形的面积相等,可知S△BDM=S△ABM,S△CDN=S△BDN,
可知S△BDM+S△BDN=S△ABM+S△CDN=$\frac{1}{2}$S四边形ABCD,
∴四边形BNDM的面积S1和四边形ABCD面积S之间的关系是1:2.
故答案为:1:2.
(2)如图③,连结BD,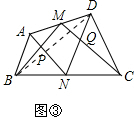
根据三角形面积公式S=$\frac{1}{2}$ah,
△ABN和△MBN面积相等;△PBN面积为重叠面积;
△MCN和△DCN面积相等;△QCN面积为重叠面积;
可得:△ABP+△DCQ面积和等于△MPN+△MQN,等于36.
答:两个三角形ABP、DCQ的面积和是36.
点评 考查了面积及等级变换的知识,解答本题的关键是等底等高的三角形的面积相等,难点在于利用(1)中材料得到三角形的面积相等,难点不大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.方程组$\left\{\begin{array}{l}{x+y=10}\\{2x+y=16}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=6}\\{y=4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=4}\\{y=8}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=4}\\{y=6}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=9}\\{y=-1}\end{array}\right.$ |
 如图,宽度为1的两个长方形纸条所交锐角为60°,则两纸条重叠部分的面积是$\frac{2}{3}\sqrt{3}$.
如图,宽度为1的两个长方形纸条所交锐角为60°,则两纸条重叠部分的面积是$\frac{2}{3}\sqrt{3}$.