题目内容
6.在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动(不与点C重合),点Q从C点出发沿CB边向点B以2cm/s的速度移动(不与点B重合).如果P、Q同时出发,x秒钟后,四边形APQB的面积为y平方厘米,y与x的函数图象大致是( )| A. | 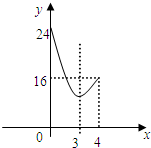 | B. | 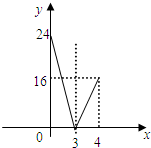 | ||
| C. | 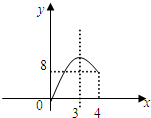 | D. | 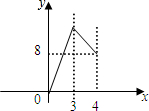 |
分析 设P、Q同时出发,x秒钟后,AP=xcm,PC=(6-x)cm,CQ=2xcm,此时△PCQ的面积为:$\frac{1}{2}$×2x(6-x),根据四边形APQB的面积y=△ABC的面积-△PCQ的面积,列出函数表达式即可作出判断.
解答 解:设P、Q同时出发,x秒钟后,AP=xcm,PC=(6-x)cm,CQ=2xcm,
则△PCQ的面积为:$\frac{1}{2}$×2x(6-x),
∴四边形APQB的面积y=$\frac{1}{2}$×6×8-$\frac{1}{2}$×2x(6-x)=x2-6x+24(0<x≤4).
故选:A.
点评 本题主要考查了动点问题的函数图象,根据题意列出函数表达式是解决问题的关键.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
11.下列调查中,适合全面调查的是( )
| A. | 了解旬河水中汞含量是否符合规定标准 | |
| B. | 了解县师训教研中心36名员工的健康状况 | |
| C. | 商家为了解某一批“电子白板”的使用寿命 | |
| D. | 为了解空气中PM2.5含量 |
15.下面4个点中,哪个点在直线y=-2x+3上( )
| A. | (-1,1) | B. | (1,-1) | C. | (2,-1) | D. | (5,13) |
 如图所示,已知a∥b,AB⊥a,∠1=50°,∠2=65°,求∠3和∠4的度数.
如图所示,已知a∥b,AB⊥a,∠1=50°,∠2=65°,求∠3和∠4的度数.