题目内容
9.已知a2+a-1=0,a4+a-4=7.分析 已知等式两边除以a变形后,两边平方求出a2+$\frac{1}{{a}^{2}}$的值,再两边平方即可求出所求式子的值.
解答 解:已知等式变形得:a-$\frac{1}{a}$=-1,
两边平方得:(a-$\frac{1}{a}$)2=a2+$\frac{1}{{a}^{2}}$-2=1,即a2+$\frac{1}{{a}^{2}}$=3,
两边平方得:(a2+$\frac{1}{{a}^{2}}$)2=a4+$\frac{1}{{a}^{4}}$+2=9,
则a4+a-4=a4+$\frac{1}{{a}^{4}}$=7.
故答案为:7.
点评 此题考查了完全平方公式、分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
 如图,AB=AC,则点C表示的数是2-$\sqrt{3}$.
如图,AB=AC,则点C表示的数是2-$\sqrt{3}$. 如图所示,已知a∥b,AB⊥a,∠1=50°,∠2=65°,求∠3和∠4的度数.
如图所示,已知a∥b,AB⊥a,∠1=50°,∠2=65°,求∠3和∠4的度数.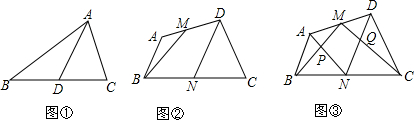
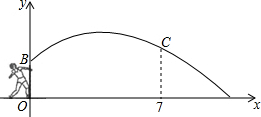 如图是医学生投掷铅球时,铅球运行的高度y(m)与水平距离x(m)的函数图象,其解析式为y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{3}{5}$.
如图是医学生投掷铅球时,铅球运行的高度y(m)与水平距离x(m)的函数图象,其解析式为y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{3}{5}$.