题目内容
8.若点A(3,8)、B(-4,m)在同一个反比例函数的图象上,则m的值为-6.分析 设反比例函数的解析式为y=$\frac{k}{x}$(k为常数,k≠0),把A(3,8)代入函数解析式求出k,得出函数解析式,把B点的坐标代入,即可求出答案.
解答 解:设反比例函数的解析式为y=$\frac{k}{x}$(k为常数,k≠0),
把A(3,8)代入函数解析式得:k=24,
即y=$\frac{24}{x}$,
把B点的坐标代入得:m=$\frac{24}{-4}$=-6,
故答案为:-6.
点评 本题考查了反比例函数图象上点的坐标特征,用待定系数法求函数解析式的应用,能求出函数解析式是解此题的关键,数形结合思想的应用.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
18.小林在某商店购买商品A,B共三次,只有其中一次购买时,商品A,B同时打折,其余两次均按标价购买,三次购买商品A、B的数量和费用如表所示,
(1)在这三次购物中,第三次购物打了折扣;
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?
| 购买商品A的数量/个 | 购买商品B的数量/个 | 购买总费用/元 | |
| 第一次购物 | 6 | 5 | 1140 |
| 第二次购物 | 3 | 7 | 1110 |
| 第三次购物 | 9 | 8 | 1062 |
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?
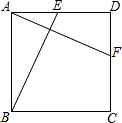 如图,在正方形ABCD中,点E,F分别在AD,CD上,且AE=DF,连接BE,AF.求证:BE=AF.
如图,在正方形ABCD中,点E,F分别在AD,CD上,且AE=DF,连接BE,AF.求证:BE=AF. 如图,点A、B的坐标分别为(1,1)和(5,4),抛物线y=ax2+bx+c(a≠0)的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),当抛物线的顶点为A时,点C的横坐标为O,则点D的横坐标最大值为( )
如图,点A、B的坐标分别为(1,1)和(5,4),抛物线y=ax2+bx+c(a≠0)的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),当抛物线的顶点为A时,点C的横坐标为O,则点D的横坐标最大值为( )