题目内容
3.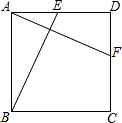 如图,在正方形ABCD中,点E,F分别在AD,CD上,且AE=DF,连接BE,AF.求证:BE=AF.
如图,在正方形ABCD中,点E,F分别在AD,CD上,且AE=DF,连接BE,AF.求证:BE=AF.
分析 根据正方形的四条边都相等可得AB=AD,每一个角都是直角可得∠BAE=∠D=90°,然后利用“边角边”证明△ABE和△ADF全等,根据全等三角形对应边相等证明即可.
解答 证明:在正方形ABCD中,AB=AD,∠BAE=∠D=90°,
在△ABE和△ADF中,
$\left\{\begin{array}{l}{AB=AD}\\{∠BAE=∠D=90°}\\{AE=DF}\end{array}\right.$,
∴△ABE≌△ADF(SAS),
∴BE=AF.
点评 本题考查了正方形的性质,全等三角形的判定与性质,掌握三角形全等的判定方法与正方形的性质是解题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
14.在数轴上与原点的距离小于5的点对应的x满足( )
| A. | -5<x<5 | B. | x<5 | C. | x<-5或x>5 | D. | x>5 |
11.下列判断中,你认为正确的是( )
| A. | 0的倒数是0 | B. | π是有理数 | C. | $\sqrt{5}$大于2 | D. | $\sqrt{9}$的值是±3 |
13.下列说法正确的是( )
| A. | 平角是一条直线 | B. | 角的边越长,角越大 | ||
| C. | 大于直角的角叫做钝角 | D. | 两个锐角的和不一定是钝角 |
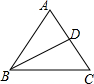 在△ABC中,AB=AC=5,BC=6,BD平分∠ABC.将△ABD沿BD折叠,点A落在A′处,则△DA′C的面积是$\frac{12}{11}$.
在△ABC中,AB=AC=5,BC=6,BD平分∠ABC.将△ABD沿BD折叠,点A落在A′处,则△DA′C的面积是$\frac{12}{11}$.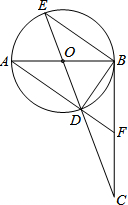 如图,AB是⊙O的直径,BC⊥AB,垂足为点B,连接CO并延长交⊙O于点D、E,连接AD并延长交BC于点F.则下列结论正确的有( )
如图,AB是⊙O的直径,BC⊥AB,垂足为点B,连接CO并延长交⊙O于点D、E,连接AD并延长交BC于点F.则下列结论正确的有( )