题目内容
2．先化简，再求值：$\frac{x-1}{{x}^{2}-4x+4}$÷（1+$\frac{1}{x-2}$），其中x=-3．分析 先将代数式$\frac{x-1}{{x}^{2}-4x+4}$÷（1+$\frac{1}{x-2}$）进行化简，然后将x=-3代入求解即可．
解答 解：$\frac{x-1}{{x}^{2}-4x+4}$÷（1+$\frac{1}{x-2}$）
=$\frac{x-1}{（x-2）^{2}}$÷$\frac{x-1}{x-2}$
=$\frac{x-1}{（x-2）^{2}}$×$\frac{x-2}{x-1}$
=$\frac{1}{x-2}$．
当x=-3时，
原式=$\frac{1}{-3-2}$=-$\frac{1}{5}$．
点评 本题考查了分式的化简求值，解答本题的关键在于先将代数式$\frac{x-1}{{x}^{2}-4x+4}$÷（1+$\frac{1}{x-2}$）进行化简，然后将x=-3代入求解．
练习册系列答案
相关题目
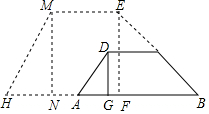如图，拦水坝的横断面为梯形ABCD，AB∥CD，坝顶宽DC为6米，坝高DG为2米，迎水坡BC的坡角为30°，坝底宽AB为（8+2$\sqrt{3}$）米．