题目内容
12.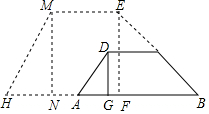 如图,拦水坝的横断面为梯形ABCD,AB∥CD,坝顶宽DC为6米,坝高DG为2米,迎水坡BC的坡角为30°,坝底宽AB为(8+2$\sqrt{3}$)米.
如图,拦水坝的横断面为梯形ABCD,AB∥CD,坝顶宽DC为6米,坝高DG为2米,迎水坡BC的坡角为30°,坝底宽AB为(8+2$\sqrt{3}$)米.(1)求背水坡AD的坡度;
(2)为了加固拦水坝,需将水坝加高2米,并且保持坝顶宽度不变,迎水坡和背水坡的坡度也不变,求加高后坝底HB的宽度.
分析 (1)作CP⊥AB于点P,即可知四边形CDGP是矩形,从而得CP=DG=2、CD=GP=6,由BP=$\frac{CP}{tanB}$=2$\sqrt{3}$根据AG=AB-GP-BP可得DG:AG=1:1;
(2)根据题意得EF=MN=4、ME=CD=6、∠B=30°,由BF=$\frac{EF}{tanB}$、HN=$\frac{MN}{tanH}$、NF=ME,根据HB=HN+NF+BF可得答案.
解答 解:(1)如图,过点C作CP⊥AB于点P,
则四边形CDGP是矩形,
∴CP=DG=2,CD=GP=6,
∵∠B=30°,
∴BP=$\frac{CP}{tanB}$=$\frac{2}{\frac{\sqrt{3}}{3}}$=2$\sqrt{3}$,
∴AG=AB-GP-BP=8+2$\sqrt{3}$-6-2$\sqrt{3}$=2=DG,
∴背水坡AD的坡度DG:AG=1:1;
(2)由题意知EF=MN=4,ME=CD=6,∠B=30°,
则BF=$\frac{EF}{tanB}$=$\frac{4}{\frac{\sqrt{3}}{3}}$=4$\sqrt{3}$,HN=$\frac{MN}{tanH}$=$\frac{4}{1}$=4,NF=ME=6,
∴HB=HN+NF+BF=4+6+4$\sqrt{3}$=10+4$\sqrt{3}$,
答:加高后坝底HB的宽度为(10+4$\sqrt{3}$)米.
点评 本题主要考查解直角三角形的应用,掌握坡度是坡面的铅直高度h和水平宽度l的比,又叫做坡比,它是一个比值,反映了斜坡的陡峭程度是解题的关键.

练习册系列答案
相关题目
4.“石家庄市明天降水概率是10%”,对此消息的下列说法正确的是( )
| A. | 石家庄市明天将有10%的地区降水 | B. | 石家庄市明天将有10%的时间降水 | ||
| C. | 石家庄市明天降水的可能性较小 | D. | 石家庄明天肯定不降水 |
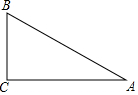 如图,坡面AB的长为40米,坡面的铅垂高度BC为20米.求坡面的坡度和坡角α的度数.
如图,坡面AB的长为40米,坡面的铅垂高度BC为20米.求坡面的坡度和坡角α的度数.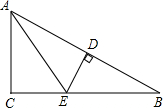 如图,∠ACB=90°,DE垂直平分AB,∠CAE=∠EAB,求∠B的度数.
如图,∠ACB=90°,DE垂直平分AB,∠CAE=∠EAB,求∠B的度数.