题目内容
11. 如图,点D、E分别在AB、AC上,且∠ABC=∠AED,若DE=4,AE=5,BC=8,求AB的长.
如图,点D、E分别在AB、AC上,且∠ABC=∠AED,若DE=4,AE=5,BC=8,求AB的长.
分析 由∠ABC=∠AED,∠A是公共角,易证得△ADE∽△ACB,然后由相似三角形的对应边成比例,求得AB的长.
解答 解:∵∠ABC=∠AED,∠A=∠A,
∴△ADE∽△ACB,
∴$\frac{AE}{AB}$=$\frac{DE}{BC}$,
∵DE=4,AE=5,BC=8,
∴$\frac{5}{AB}$=$\frac{4}{8}$,
解得:AB=10.
点评 此题考查了相似三角形的判定与性质.注意证得△ADE∽△ACB是解此题的关键.

练习册系列答案
相关题目
19.不解方程,判别方程2x2-2$\sqrt{2}$x+1=0根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |
6. 如图,二次函数y=-x2+2x+3的图象与x轴交于点A和点B,顶点为C,AC与y轴交于点D,则$\frac{OD}{AD}$=( )
如图,二次函数y=-x2+2x+3的图象与x轴交于点A和点B,顶点为C,AC与y轴交于点D,则$\frac{OD}{AD}$=( )
 如图,二次函数y=-x2+2x+3的图象与x轴交于点A和点B,顶点为C,AC与y轴交于点D,则$\frac{OD}{AD}$=( )
如图,二次函数y=-x2+2x+3的图象与x轴交于点A和点B,顶点为C,AC与y轴交于点D,则$\frac{OD}{AD}$=( )| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | 2 | D. | $\frac{1}{2}$ |
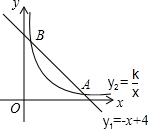 如图,函数y1=-x+4的图象与函数y2=$\frac{k}{x}$(x>0)的图象交于A(a,1)、B(1,b)两点.
如图,函数y1=-x+4的图象与函数y2=$\frac{k}{x}$(x>0)的图象交于A(a,1)、B(1,b)两点. 有理数a,b,c表示的点在数轴上的位置如图所示,
有理数a,b,c表示的点在数轴上的位置如图所示,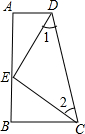 如图,DA⊥AB于点A,CB⊥AB于点B,E是AB上一点,且BC=AE,∠1=∠2,则:
如图,DA⊥AB于点A,CB⊥AB于点B,E是AB上一点,且BC=AE,∠1=∠2,则: 小明家离学校5千米,放学后,爸爸从家里出发去学校接小明,与此同时小明从学校出发往家走,已知爸爸的速度是6千米/小时,小明的速度是4千米/小时.
小明家离学校5千米,放学后,爸爸从家里出发去学校接小明,与此同时小明从学校出发往家走,已知爸爸的速度是6千米/小时,小明的速度是4千米/小时.