题目内容
1．
小明家离学校5千米，放学后，爸爸从家里出发去学校接小明，与此同时小明从学校出发往家走，已知爸爸的速度是6千米/小时，小明的速度是4千米/小时．（1）爸爸与小明相遇时，爸爸走了多少时间？
（2）若小明出发20分钟后发现书本忘带了，立刻转身以8千米/小时的速度返回学校拿到书本后仍以此速度继续往家走．请问爸爸与小明相遇时，离学校还有多远？（不计途中耽搁）
分析 （1）根据爸爸的速度是6千米/小时，小明的速度是4千米/小时，小明家离学校5千米，利用两人行走的和为5千米列出方程求解即可；
（2）设爸爸走了y小时，等量关系是：爸爸y小时行走的路程+小明以8千米/小时的速度行走（y-$\frac{1}{3}$）小时的路程-小明以4千米/小时的速度行走$\frac{1}{3}$小时的路程=5千米，依此列出方程求解即可．
解答 解：（1）设爸爸走了x小时．
根据题意，得 （6+4）x=5，
解得：x=$\frac{1}{2}$，
答：爸爸走了$\frac{1}{2}$小时．
（2）设爸爸走了y小时，20分钟=$\frac{1}{3}$小时，
根据题意得：6y+8（y-$\frac{1}{3}$）-4×$\frac{1}{3}$=5，
解得：y=$\frac{9}{14}$，
则5-6×$\frac{9}{14}$=$\frac{8}{7}$（千米）．
答：爸爸与小明相遇时，离学校还有$\frac{8}{7}$千米远．
点评 此题主要考查了一元一次方程在行程问题中的应用，利用两人行走的速度与时间得出方程是解题的关键．
练习册系列答案
相关题目
如图，点D、E分别在AB、AC上，且∠ABC=∠AED，若DE=4，AE=5，BC=8，求AB的长．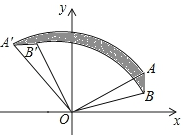
如图，已知A（2$\sqrt{3}$，2）、B（2$\sqrt{3}$，1），将△AOB绕着点O逆时针旋转，使点A旋转到点A′（-2，2$\sqrt{3}$）的位置，B旋转到点B′位置．
6．下列变形正确的是（ ）
| A． | $\frac{{x}^{6}}{{x}^{2}}$=x3 | B． | $\frac{-x+y}{x-y}$=-1 | C． | $\frac{{x}^{2}+{y}^{2}}{x+y}$=x+y | D． | $\frac{x+2}{x+3}$=$\frac{2}{3}$ |