题目内容
16.(1)计算:${(\frac{1}{3})^{-2}}-|{-3}|-{(2012-π)^0}+\root{3}{64}$(2)化简:$\frac{a^2}{a+1}-\frac{1}{a+1}$.
分析 (1)原式第一项利用负整数指数幂法则计算,第二项利用绝对值的代数意义化简,第三项利用零指数幂法则计算,最后一项利用立方根定义计算即可得到结果;
(2)原式利用同分母分式的减法法则计算,约分即可得到结果.
解答 解:(1)原式=9-3-1+4=9;
(2)原式=$\frac{{a}^{2}-1}{a+1}$=$\frac{(a+1)(a-1)}{a+1}$=a-1.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
1.下列满足两根之和为2的一元二次方程的方程是( )
| A. | x2-2x+4=0 | B. | x2-2x-1=0 | C. | 2x2-2x-5=0 | D. | x2+2x-1=0 |
8.下列说法正确的是( )
| A. | $\frac{πx}{5}$的系数是$\frac{1}{5}$ | B. | $\frac{3x-1}{3}$是单项式 | ||
| C. | -25m是5次单项式 | D. | -x2y-35xy3是四次多项式 |
5. 如图,如果直线是多边形的对称轴,其中∠A=130°,∠B=110°,那么∠BCD的度数等于( )
如图,如果直线是多边形的对称轴,其中∠A=130°,∠B=110°,那么∠BCD的度数等于( )
 如图,如果直线是多边形的对称轴,其中∠A=130°,∠B=110°,那么∠BCD的度数等于( )
如图,如果直线是多边形的对称轴,其中∠A=130°,∠B=110°,那么∠BCD的度数等于( )| A. | 60° | B. | 50° | C. | 40° | D. | 70° |
6.下列变形正确的是( )
| A. | $\frac{{x}^{6}}{{x}^{2}}$=x3 | B. | $\frac{-x+y}{x-y}$=-1 | C. | $\frac{{x}^{2}+{y}^{2}}{x+y}$=x+y | D. | $\frac{x+2}{x+3}$=$\frac{2}{3}$ |
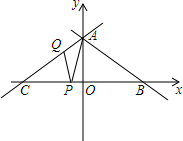 如图,直线AB:y=-$\frac{\sqrt{3}}{3}$x+$\frac{8\sqrt{3}}{3}$交坐标轴于A、B两点,直线AC与AB关于y轴对称,交x轴于点C.点P、Q分别是线段BC、AC上两个动点,且∠APQ始终等于30°.
如图,直线AB:y=-$\frac{\sqrt{3}}{3}$x+$\frac{8\sqrt{3}}{3}$交坐标轴于A、B两点,直线AC与AB关于y轴对称,交x轴于点C.点P、Q分别是线段BC、AC上两个动点,且∠APQ始终等于30°. 如图,点D、E分别在AB、AC上,且∠ABC=∠AED,若DE=4,AE=5,BC=8,求AB的长.
如图,点D、E分别在AB、AC上,且∠ABC=∠AED,若DE=4,AE=5,BC=8,求AB的长.