题目内容
11.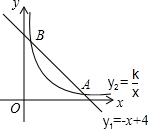 如图,函数y1=-x+4的图象与函数y2=$\frac{k}{x}$(x>0)的图象交于A(a,1)、B(1,b)两点.
如图,函数y1=-x+4的图象与函数y2=$\frac{k}{x}$(x>0)的图象交于A(a,1)、B(1,b)两点.(1)求k的值;
(2)利用图象分别写出当x>1时,
①y1和y2的取值范围;
②y1和y2的大小关系.
分析 (1)把A(a,1)代入y1=-x+4求得a,进一步代入函数y2=$\frac{k}{x}$求得k即可;
(2)求得b,利用图象得出答案即可.
解答 解:(1)把点A(a,1)代入y1=-x+4,得a=3,
则1=$\frac{k}{3}$,k=3;
(2)把点B(1,b)代入y=$\frac{3}{x}$,得出b=3;
如图,
由图象可知:
①x>1时,y1<3,0<y2<3;
②当1<x<3时,y1>y2;
当x=1或x=3时,y1=y2;
当x>3时,y1<y2.
点评 本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了待定系数法求函数解析式以及观察函数图象的能力.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
2.函数y=(k2+2k)xk2+k-1是反比例函数,则k的值为( )
| A. | 1 | B. | -1 | C. | 0或-1 | D. | ±1 |
6. 如图,一圆柱高为8cm,底面周长为30cm,蚂蚁在圆柱表面爬行,从点A爬到点B的最短路程是( )
如图,一圆柱高为8cm,底面周长为30cm,蚂蚁在圆柱表面爬行,从点A爬到点B的最短路程是( )
 如图,一圆柱高为8cm,底面周长为30cm,蚂蚁在圆柱表面爬行,从点A爬到点B的最短路程是( )
如图,一圆柱高为8cm,底面周长为30cm,蚂蚁在圆柱表面爬行,从点A爬到点B的最短路程是( )| A. | 15cm | B. | 17cm | C. | 18cm | D. | 30cm |
 已知P(-3,m)和 Q(1,m)是抛物线y=x2+bx-3上的两点.
已知P(-3,m)和 Q(1,m)是抛物线y=x2+bx-3上的两点.
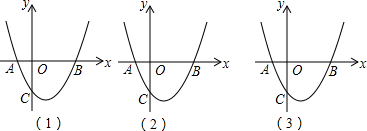
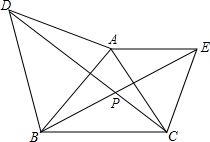 如图,△ABC中,分别以AB、AC为边向外作正△ABD、△ACE.试说明:
如图,△ABC中,分别以AB、AC为边向外作正△ABD、△ACE.试说明: 如图,点D、E分别在AB、AC上,且∠ABC=∠AED,若DE=4,AE=5,BC=8,求AB的长.
如图,点D、E分别在AB、AC上,且∠ABC=∠AED,若DE=4,AE=5,BC=8,求AB的长.