题目内容
用适当的方法解下列方程
(1)x2+2x-2=0(用配方法解)
(2)x2+2
x+3=0
(3)3x2+4x=7.
(1)x2+2x-2=0(用配方法解)
(2)x2+2
| 3 |
(3)3x2+4x=7.
考点:解一元二次方程-因式分解法,解一元二次方程-配方法
专题:
分析:(1)用配方法解答;
(2)根据完全平方公式解答;
(3)用十字相乘法解答.
(2)根据完全平方公式解答;
(3)用十字相乘法解答.
解答:解:(1)x2+2x-2=0(用配方法解),
移项,得x2+2x=2,
配方,得x2+2x+1=2+1,
(x+1)2=3,
开方,得x+1=±
x1=-1+
,x2=-1-
.
(2)x2+2
x+3=0
配方,得(x+
)2=0,
开方,得x+
=0,
解得x1=x2=-
.
(3)3x2+4x=7,
方程可化为3x2+4x-7=0,
(x-1)(3x+7)=0,
解得x-1=0,3x+7=0,
x1=1;x2=-
.
移项,得x2+2x=2,
配方,得x2+2x+1=2+1,
(x+1)2=3,
开方,得x+1=±
| 3 |
x1=-1+
| 3 |
| 3 |
(2)x2+2
| 3 |
配方,得(x+
| 3 |
开方,得x+
| 3 |
解得x1=x2=-
| 3 |
(3)3x2+4x=7,
方程可化为3x2+4x-7=0,
(x-1)(3x+7)=0,
解得x-1=0,3x+7=0,
x1=1;x2=-
| 7 |
| 3 |
点评:本题考查了一元二次方程的解法,根据式子的结构,利用适当的方法是解题的关键.

练习册系列答案
相关题目
下列各式可以用完全平方公式分解因式的是( )
| A、x2-4x+4 |
| B、1+4x2 |
| C、4y2+4y-1 |
| D、x2+xy+y2 |
 如图,量角器上的C、D两点所表示的读数分别是80°、50°,则∠DBC的度数为
如图,量角器上的C、D两点所表示的读数分别是80°、50°,则∠DBC的度数为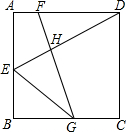 如图,在正方形ABCD中,点E是AB上一点,G是BC上一点,FG⊥DE交于点H,FG=DE,求证:FD+EG≥
如图,在正方形ABCD中,点E是AB上一点,G是BC上一点,FG⊥DE交于点H,FG=DE,求证:FD+EG≥ 如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交AB于E,交⊙O于D.求弦CB、AD的长.
如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交AB于E,交⊙O于D.求弦CB、AD的长. 如图所示,△ABC为直角三角形,∠ACB=90°,若∠A=30°,那么线段BC、AB的长度有何数量关系?
如图所示,△ABC为直角三角形,∠ACB=90°,若∠A=30°,那么线段BC、AB的长度有何数量关系?