题目内容
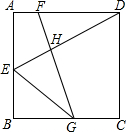 如图,在正方形ABCD中,点E是AB上一点,G是BC上一点,FG⊥DE交于点H,FG=DE,求证:FD+EG≥
如图,在正方形ABCD中,点E是AB上一点,G是BC上一点,FG⊥DE交于点H,FG=DE,求证:FD+EG≥| 2 |
考点:正方形的性质,全等三角形的判定与性质,等腰直角三角形,平移的性质
专题:
分析:平移FG,使点F与点D重合,交BC的延长线于点I,证得△ADE≌△DCI,得出ED=DI=FG,平移DE至FL,使D与F重合,连接LG,进一步得出△FLG是等腰直角三角形,从而得出LG=
FG,进而求得FD+EG=LE+EG≥LG=
FG.
| 2 |
| 2 |
解答: 解:平移FG,使F与A重合,G移到K点,
解:平移FG,使F与A重合,G移到K点,
∴AK∥FG,AK=FG,
∵四边形ABCD是正方形,
∴AD=AB,
∵FG⊥DE,AK∥FG,
∴AK⊥DE,
∴∠BAK=∠ADE,
在△ADE和△BAK中,
,
∴△ADE≌△BAK(AAS),
∴ED=AK=FG,
平移DE至FL,使D与F重合,连接LG,
∴FL∥DE,FL=DE,
∴FL=FG,∠LFG=∠EHG=90°,
∴△FLG是等腰直角三角形,
∴LG=
FG,
∵FD=LE,
∴FD+EG=LE+EG≥LG=
FG.
故FD+EG≥
FG.
 解:平移FG,使F与A重合,G移到K点,
解:平移FG,使F与A重合,G移到K点,∴AK∥FG,AK=FG,
∵四边形ABCD是正方形,
∴AD=AB,
∵FG⊥DE,AK∥FG,
∴AK⊥DE,
∴∠BAK=∠ADE,
在△ADE和△BAK中,
|
∴△ADE≌△BAK(AAS),
∴ED=AK=FG,
平移DE至FL,使D与F重合,连接LG,
∴FL∥DE,FL=DE,
∴FL=FG,∠LFG=∠EHG=90°,
∴△FLG是等腰直角三角形,
∴LG=
| 2 |
∵FD=LE,
∴FD+EG=LE+EG≥LG=
| 2 |
故FD+EG≥
| 2 |
点评:本题考查了正方形的性质,平移的性质,全等三角形的判定和性质,等腰直角三角形的判定和性质,平移得到平行四边形是解题的关键.

练习册系列答案
相关题目
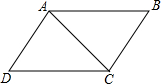 如图,已知△ABC≌△CDA,A和C,D和B分别是对应点,如果AB=7cm,AD=
如图,已知△ABC≌△CDA,A和C,D和B分别是对应点,如果AB=7cm,AD=6cm,AC=4cm,则DC的长为( )
| A、6cm | B、7cm |
| C、4cm | D、不确定 |
 如图,矩形ABCD中,AB=3cm,AD=9cm,过对角线BD的中点O作BD的垂直平分线EF分别交AD,BC于E,F,则EF长为
如图,矩形ABCD中,AB=3cm,AD=9cm,过对角线BD的中点O作BD的垂直平分线EF分别交AD,BC于E,F,则EF长为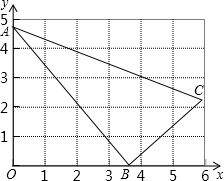 如图,△ABC中,∠ABC=90°,A(0,4.8),B(3.6,0).BC=3,
如图,△ABC中,∠ABC=90°,A(0,4.8),B(3.6,0).BC=3,