题目内容
8. 如图,PA、PB是⊙O的切线,CD切⊙O于E,PA=6,∠APB=60°.求:
如图,PA、PB是⊙O的切线,CD切⊙O于E,PA=6,∠APB=60°.求:(1)△PDC的周长;
(2)⊙O的半径;
(3)∠COD的度数.
分析 (1)通过切线长定理将相等的线段进行转换,得出三角形PDE的周长等于PA+PB即可得出答案;
(2)根据切线长定理得出∠OPA=30°,可知OP=2OA,再利用勾股定理求出圆的半径;
(3)根据切线的性质和∠APB=60°,可知∠AOB=120°,再根据切线长定理可知OC、OD分别平分∠AOE、∠BOE,于是∠COD=$\frac{1}{2}$∠AOB=60°.
解答 解:(1)∵CA,CE都是圆O的切线,
∴CA=CE,
同理DE=DB,PA=PB,
∴△PDC的周长=PD+CD+PC=PD+PC+CA+BD=PA+PB=2PA=12;
(2)连接OA,OP,则OA⊥PA,
∵PA、PB是⊙O的切线,
∴∠APO=$\frac{1}{2}$∠APB=30°,
∴在Rt△AOP中,PO=2AO,
故OA2+62=(2AO)2,
解得:OA=2$\sqrt{3}$,
∴⊙O的半径为2$\sqrt{3}$;
(3)∵PA、PB是⊙O的切线,
∴∠PAO=∠PBO=90°,
∵∠APB=60°,
∴∠AOB=120°,
根据切线长定理可知OC、OD分别平分∠ACE、∠BDE,
∴OC、OD分别平分∠AOE、∠BOE,
∴∠COD=$\frac{1}{2}$∠AOB=60°.
点评 本题考查了切线长定理,运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
16.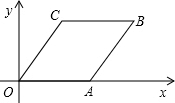 如图,?OABC的顶点O、A、C的坐标分别是(0,0),(2,0),(0.5,1),则点B的坐标是( )
如图,?OABC的顶点O、A、C的坐标分别是(0,0),(2,0),(0.5,1),则点B的坐标是( )
 如图,?OABC的顶点O、A、C的坐标分别是(0,0),(2,0),(0.5,1),则点B的坐标是( )
如图,?OABC的顶点O、A、C的坐标分别是(0,0),(2,0),(0.5,1),则点B的坐标是( )| A. | (1,2) | B. | (0.5,2) | C. | (2.5,1) | D. | (2,0.5) |
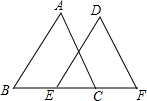 将△ABC沿直线BC平移,得到△DEF(如图).求证:
将△ABC沿直线BC平移,得到△DEF(如图).求证: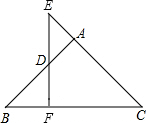 如图,在△ABC中,AB=AC,D为AB上一动点,作DF⊥BC于F,交CA的延长线于E.
如图,在△ABC中,AB=AC,D为AB上一动点,作DF⊥BC于F,交CA的延长线于E.