题目内容
18.若x,y都是实数,则x2+xy+y2-3x-3y+1999的最小值是1996.分析 首先设x=a+b,y=a-b,通过拆分项、完全平方式转化为3(a-1)2+b2+1996,再根据非负数的性质,即可得解.
解答 解:设x=a+b,y=a-b,
原式=(a+b)2+(a-b)2+(a+b)(a-b)-3(a+b)-3(a-b0+1999
=a2+b2+2ab+b2+a2-2ab+a2-b2-3a-3b-3a+3b+1999
=3a2+b2-6a+1999
=3a2-6a+3+b2+1996
=3(a-1)2+b2+1996≥1996,
∴最小值是1996.
故答案为:1996.
点评 本题考查配方法的运用,完全平方式,非负数的性质,掌握完全平方公式是解决问题的关键.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
 如图是抛物线形拱桥,当水面在l时.拱顶离水面2m.水面宽8m.水面下降0.25m.水面宽度增加多少?
如图是抛物线形拱桥,当水面在l时.拱顶离水面2m.水面宽8m.水面下降0.25m.水面宽度增加多少?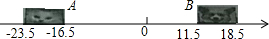 七年级小贝在-张纸上画了-条数轴,妹妹不知它有什么用,就在上面画了一只小猫和一只小狗,于是数轴上标的数字有的看不到了,请根据数轴回答下列问题:
七年级小贝在-张纸上画了-条数轴,妹妹不知它有什么用,就在上面画了一只小猫和一只小狗,于是数轴上标的数字有的看不到了,请根据数轴回答下列问题: 如图,在?ABCD中,点E是BC的中点,AE、BD相交于点O.
如图,在?ABCD中,点E是BC的中点,AE、BD相交于点O. 如图,点A、B、C、D、E在⊙O上,且$\widehat{AE}$为40°,求∠B+∠D的度数.
如图,点A、B、C、D、E在⊙O上,且$\widehat{AE}$为40°,求∠B+∠D的度数. 如图,△ABC绕点B旋转后,顶点C的对应点D.请确定△ABC旋转后的三角形.
如图,△ABC绕点B旋转后,顶点C的对应点D.请确定△ABC旋转后的三角形. 如图,PA、PB是⊙O的切线,CD切⊙O于E,PA=6,∠APB=60°.求:
如图,PA、PB是⊙O的切线,CD切⊙O于E,PA=6,∠APB=60°.求: