题目内容
17.(1)在s=vt中,已知s,t,则v=$\frac{s}{t}$;已知s,v,则t=$\frac{s}{v}$.(2)已知$\frac{1}{u}$+$\frac{1}{v}$=$\frac{1}{f}$(uvf≠0),则f=$\frac{uv}{v+u}$.
分析 (1)方程两边都除以t,方程两边都除以v,即可得出答案;
(2)先通分,再求出倒数即可.
解答 解:(1)s=vt,
v=$\frac{s}{t}$,t=$\frac{s}{v}$,
故答案为:$\frac{s}{t}$,$\frac{s}{v}$;
(2)$\frac{1}{u}$+$\frac{1}{v}$=$\frac{1}{f}$,
$\frac{1}{f}$=$\frac{v+u}{uv}$,
f=$\frac{uv}{v+u}$,
故答案为:$\frac{uv}{v+u}$.
点评 本题考查了分式的混合运算,倒数,等式的基本性质的应用,能正确根据等式的基本性质进行变形是解此题的关键,难度不是很大.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
5.若分式$\frac{1-b}{2{b}^{2}+1}$的值是负数,则b满足( )
| A. | b<0 | B. | b≥1 | C. | b<1 | D. | b>1 |
 如图,△ABC绕点B旋转后,顶点C的对应点D.请确定△ABC旋转后的三角形.
如图,△ABC绕点B旋转后,顶点C的对应点D.请确定△ABC旋转后的三角形. 如图,PA、PB是⊙O的切线,CD切⊙O于E,PA=6,∠APB=60°.求:
如图,PA、PB是⊙O的切线,CD切⊙O于E,PA=6,∠APB=60°.求: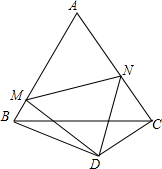 已知,如图,△ABC是等边三角形,BD=DC,∠BDC=120°,∠MDN=60°,求证:C△AMN=$\frac{2}{3}$•C△ABC.(提示:先证:MN=BM+NC)
已知,如图,△ABC是等边三角形,BD=DC,∠BDC=120°,∠MDN=60°,求证:C△AMN=$\frac{2}{3}$•C△ABC.(提示:先证:MN=BM+NC) 如图所示,过正方形ABCD的顶点A在正方形ABCD的内部作∠EAF=45°,E、F分别在BC、CD上,连接EF,作AH⊥EF于点H
如图所示,过正方形ABCD的顶点A在正方形ABCD的内部作∠EAF=45°,E、F分别在BC、CD上,连接EF,作AH⊥EF于点H