题目内容
8.(1)计算:(π-3.14)0+($\frac{1}{2}$)-1+|-2$\sqrt{2}$|-$\sqrt{8}$.(2)先化简,再求值:$\frac{2x-6}{{x}^{2}+2x+1}$÷($\frac{{x}^{2}+1}{x+1}$-x+1),并从-tan60°≤x≤2cos30°取出一个合适的整数,求出式子的值.
分析 (1)根据零指数幂、负整数指数幂、绝对值可以解答本题;
(2)先化简题目中的式子,然后根据-tan60°≤x≤2cos30°,从中选取使得原分式有意义的x的整数值代入即可解答本题.
解答 解:(1)(π-3.14)0+($\frac{1}{2}$)-1+|-2$\sqrt{2}$|-$\sqrt{8}$
=1+2+2$\sqrt{2}-2\sqrt{2}$
=3;
(2)$\frac{2x-6}{{x}^{2}+2x+1}$÷($\frac{{x}^{2}+1}{x+1}$-x+1)
=$\frac{2(x-3)}{(x+1)^{2}}÷\frac{{x}^{2}+1-(x-1)(x+1)}{x+1}$
=$\frac{2(x-3)}{(x+1)^{2}}•\frac{x+1}{2}$
=$\frac{x-3}{x+1}$,
∵-tan60°≤x≤2cos30°
∴$-\sqrt{3}≤x≤\sqrt{3}$,
∴当x=1时,原式=$\frac{1-3}{1+1}$=-1.
点评 本题考查整式的分式的化简求值、实数的运算、零指数幂、负整数指数幂、绝对值,解答本题的关键是明确它们各自的计算方法.

练习册系列答案
相关题目
 如图所示,已知EF⊥AB,垂足为F,CD⊥AB,垂足为D,∠1=∠2,试判断∠AGD和∠ACB是否相等,为什么?(将解答过程补充完整)
如图所示,已知EF⊥AB,垂足为F,CD⊥AB,垂足为D,∠1=∠2,试判断∠AGD和∠ACB是否相等,为什么?(将解答过程补充完整)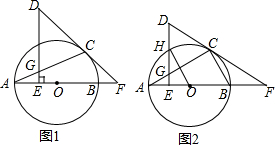
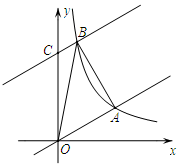 如图,在平面直角坐标系xOy中,直线y=$\frac{\sqrt{3}}{3}$x与反比例函数y=$\frac{k}{x}$在第一象限内的图象相交于点A(m,3).
如图,在平面直角坐标系xOy中,直线y=$\frac{\sqrt{3}}{3}$x与反比例函数y=$\frac{k}{x}$在第一象限内的图象相交于点A(m,3). 如图,在平面直角坐标系中,直线y=x+1与$y=-\frac{3}{4}x+3$交于点A,分别交x轴于点B和点C,点D是直线AC上的一个动点.
如图,在平面直角坐标系中,直线y=x+1与$y=-\frac{3}{4}x+3$交于点A,分别交x轴于点B和点C,点D是直线AC上的一个动点. 如图,四边形ABCD中,点E在BC上,∠A+∠ADE=180°,∠B=70°,∠C=45°,求∠EDC的度数.
如图,四边形ABCD中,点E在BC上,∠A+∠ADE=180°,∠B=70°,∠C=45°,求∠EDC的度数.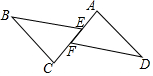 如图,点E,F在AC上,AE=CF,∠AFD=∠CEB,要使△ADF≌△CBE,需要添加的一个条件是∠A=∠C.
如图,点E,F在AC上,AE=CF,∠AFD=∠CEB,要使△ADF≌△CBE,需要添加的一个条件是∠A=∠C.