Question

3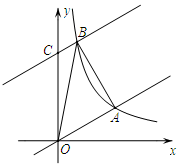．如图，在平面直角坐标系xOy中，直线y=$\frac{\sqrt{3}}{3}$x与反比例函数y=$\frac{k}{x}$在第一象限内的图象相交于点A（m，3）．
（1）求该反比例函数的关系式；
（2）将直线y=$\frac{\sqrt{3}}{3}$x沿y轴向上平移8个单位后与反比例函数在第一象限内的图象相交于点B，连接AB，这时恰好AB⊥OA，求tan∠AOB的值；
（3）在（2）的条件下，在射线OA上存在一点P，使△PAB∽△BAO，求点P的坐标．

Answer 1

分析 （1）先确定出点A坐标，再用待定系数法求出反比例函数解析式；
（2）先求出直线AB解析式，进而得出点B坐标秒即可得出结论；
（3）利用相似三角形的性质得出AP，进而求出OP，再求出∠AOH=30°，最后用含30°的直角三角形的性质即可得出结论．

解答 解：（1）∵点A（m，3）在直线y=$\frac{\sqrt{3}}{3}$x上
∴3=$\frac{\sqrt{3}}{3}$m，
∴m=3$\sqrt{3}$，
∴点A（3$\sqrt{3}$，3），
∵点A（3$\sqrt{3}$，3）在反比例函数y=$\frac{k}{x}$上，
∴k=3$\sqrt{3}$×3=9$\sqrt{3}$，
∴y=$\frac{9\sqrt{3}}{x}$；

（2）直线向上平移8个单位后表达式为：y=$\frac{\sqrt{3}}{3}$x+8
∵AB⊥OA，直线AB过点A（3$\sqrt{3}$，3）
∴直线AB解析式：y=-$\sqrt{3}$x+12，
∴$\frac{\sqrt{3}}{3}$x+8=-$\sqrt{3}$x+12，
∴x=$\sqrt{3}$．
∴B（$\sqrt{3}$，9），
∴AB=4$\sqrt{3}$
在Rt△AOB中，OA=6，
∴tan∠AOB=$\frac{4\sqrt{3}}{6}=\frac{2\sqrt{3}}{3}$

（3）如图，∵△APB∽△ABO，
∴$\frac{AP}{AB}=\frac{AB}{OA}$，
由（2）知，AB=4$\sqrt{3}$，OA=6
即$\frac{AP}{4\sqrt{3}}=\frac{4\sqrt{3}}{6}$
∴AP=8，
∵OA=6，
∴OP=14，
过点A作AH⊥x轴于H
∵A（3$\sqrt{3}$，3），
∴OH=3$\sqrt{3}$，AH=3，
在Rt△AOH中，
∴tan∠AOH=$\frac{AH}{OH}$=$\frac{3}{3\sqrt{3}}$=$\frac{\sqrt{3}}{3}$，
∴∠AOH=30°
过点P作PG⊥x轴于G，
在Rt△APG中，∠POG=30°，OP=14，
∴PG=7，OG=7$\sqrt{3}$
∴P（7$\sqrt{3}$，7）．

点评 此题是反比例函数综合题，主要考查了待定系数法，锐角三角函数的意义，相似三角形的性质，含3°角的直角三角形的性质，解（1）的关键是求出点A的坐标，解（2）的关键是求出点B的坐标，解（3）的关键是求出OP，是一道中等难度的中考常考题．