题目内容
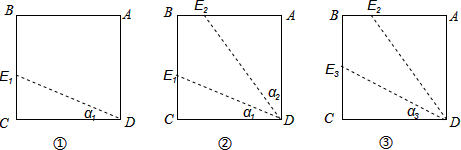
16.如图,AB是⊙O的直径,点C在⊙O上,点E在线段OA上运动,DE⊥AB,垂足为E,DE交AC于点G,DC是⊙O的切线,交AB的延长线于点F.(1)求证:∠D=2∠A;
(2)如图(2),若点E是OA的中点,点H是DE与⊙O的交点,OH∥BC,求证:△DCG是等边三角形;
(3)如图(1),若CD=2CF,且BF=1,CF=2,求CG的长.
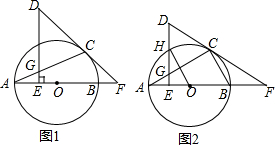
分析 (1)如图1中,连接OC,只要证明∠D=∠FOC,∠FOC=2∠A即可;
(2)如图2中,连接AH,即△AOH是等边三角形,再证明DG=DC,∠DCG=60°即可解决问题;
(3)由△FCB∽△FAC,推出CF:AF=BF:CF=CB:CA,由BF=1,CF=2,∴AF=4,推出AB=AF-BF=3,推出OB=OC=1.5,在Rt△ABC中,由CB:CA=CF:AF=1:2,AB=3,可得BC=$\frac{3\sqrt{5}}{5}$,由△DCG∽△OCB,可得$\frac{CG}{BC}=\frac{DC}{OC}$,由此求出CG即可;
解答 (1)证明:如图1中,连接OC,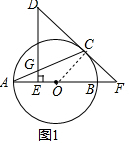
∵DC是⊙O的切线,
∴DC⊥OC,
∴∠OCF=90°,
∴∠COF+∠F=90°,
∴DE⊥AB,
∴∠D+∠F=90°,
∴∠D=∠COF,
∵∠COF=2∠A,
∴∠D=2∠A;
(2)证明:如图2中,连接AH,OC.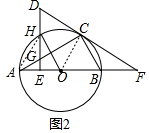
∵DE⊥AB,点E是OA的中点,
∴AH=OH,
∵OA=OH,
∴OA=OH=AH,
即△AOH是等边三角形,
∴∠AOH=60°,
∵OH∥BC,
∴∠ABC=∠AOH,
∵∠DCG=∠ABC,
∴∠DCG=∠AOH=60°,
∵OA=OC,
∴∠OAC=∠OCA,∠OAC+∠AGE=90°,∠OCA+∠DCG=90°,
∴∠AGE=∠DCG,
∵∠DGC=∠AGE,
∴∠DGC=∠DCG,
∴DG=DC,
∴△DCG是等边三角形;
(3)解:如图3中,
∵∠OCB+∠BCF=90°,∠OBC+∠A=90°
又∵OB=OC,
∴∠OCB=∠OBC,
∴∠A=∠BCF
∵∠F=∠F,
∴△FCB∽△FAC,
∴CF:AF=BF:CF=CB:CA,
∵BF=1,CF=2,
∴AF=4,
∴AB=AF-BF=3,
∴OB=OC=1.5,
在Rt△ABC中,∵CB:CA=CF:AF=1:2,AB=3,
∴BC=$\frac{3\sqrt{5}}{5}$,
∵∠D=∠BOC,∠DCG=∠OCB,
∴△DCG∽△OCB,
∴$\frac{CG}{BC}=\frac{DC}{OC}$,
∵CD=2CF,∴CD=4,
∴CG=$\frac{\frac{3\sqrt{5}}{5}•4}{1.5}$=$\frac{8\sqrt{5}}{5}$.
点评 本题考查圆综合题、等边三角形的判定和性质、相似三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题,属于中考压轴题.

 全能测控一本好卷系列答案
全能测控一本好卷系列答案| A. | 原点上 | B. | x轴正半轴上 | C. | y轴正半轴上 | D. | y轴负半轴上 |
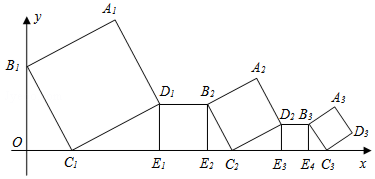
| A. | ($\frac{1}{2}$)2016 | B. | ($\frac{1}{2}$)2017 | C. | ($\frac{\sqrt{3}}{3}$)2016 | D. | ($\frac{\sqrt{3}}{3}$)2017 |
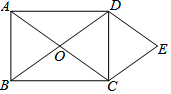 矩形ABCD对角线相交点O,DE∥AC,CE∥BD,若AD=4,CD=3,则四边形ODEC的面积为6.
矩形ABCD对角线相交点O,DE∥AC,CE∥BD,若AD=4,CD=3,则四边形ODEC的面积为6.