题目内容
11.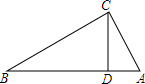 如图,在△ABC中,CD⊥AB于D,AD=9,BD=16,CD=12.
如图,在△ABC中,CD⊥AB于D,AD=9,BD=16,CD=12.(1)求△ABC的周长;
(2)△ABC是直角三角形吗?请说明理由.
分析 (1)由勾股定理求出BC、AC,即可得出结果;
(2)由勾股定理的逆定理即可得出结论.
解答 解:(1)∵CD⊥AB,
∴∠BDC=∠ADC=90°,
∴BC=$\sqrt{B{D}^{2}+C{D}^{2}}$=20,AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=15,
∵AB=AD+BD=25,
∴△ABC的周长=AB+BC+AC=25+20+15=60;
60;
(2)△ABC是直角三角形;理由如下:
∵BC2+AC2=400+225=625=252=AB2,
∴△ABC是直角三角形.
点评 本题考查了勾股定理、勾股定理的逆定理;熟练掌握勾股定理和勾股定理的逆定理,由勾股定理求出BC和AC是解决问题的关键.

练习册系列答案
相关题目
1.正方形具有而矩形不一定具有的性质是( )
| A. | 四条边相等 | B. | 对角线互相平分 | C. | 四个角相等 | D. | 对角线相等 |
15.下列各组长度的线段能构成三角形的是( )
| A. | 1.5cm,3.9cm,2.3cm | B. | 3.5cm,7.1cm,3.6cm | ||
| C. | 6cm,1cm,6cm | D. | 4cm,10cm,4cm |
19.关于x的一元二次方程mx2+(2m-1)x-2=0的根的判别式等于4,则m的值是( )
| A. | $\frac{1}{2}$ | B. | $-\frac{3}{2}$ | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$或$-\frac{3}{2}$ |
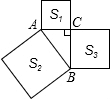 如图,已知△ABC中,∠ACB=90°,以△ABC的各边为边在△ABC外作三个正方形,S1、S2、S3分别表示这三个正方形的面积,若S1=9,S2=16,则S3=7.
如图,已知△ABC中,∠ACB=90°,以△ABC的各边为边在△ABC外作三个正方形,S1、S2、S3分别表示这三个正方形的面积,若S1=9,S2=16,则S3=7.