题目内容
3．二次函数y=-2x2+bx+1的图象与y轴的交点坐标为（0，1）．分析 计算自变量为0时的函数值即可得到抛物线与y轴的交点坐标．
解答 解：当x=0时，y=-2x2+bx+1=1，
所以二次函数y=-2x2+bx+1的图象与y轴的交点坐标为（0，1）．
故答案为（0，1）．
点评 本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．
练习册系列答案
相关题目
中
的取值范围是_____.
如图，AC∥CD，点E在BC上，若∠D=∠DEC=74°，求∠B的度数．
18．
如图，一块三角形空地上种草皮绿化，已知AB=20米，AC=30米，∠A=150°，草皮的售价为a元/米2，则购买草皮至少需要（ ）
如图，一块三角形空地上种草皮绿化，已知AB=20米，AC=30米，∠A=150°，草皮的售价为a元/米2，则购买草皮至少需要（ ）| A． | 450a元 | B． | 225a元 | C． | 150a元 | D． | 300a元 |
8．下列说法中正确的是（ ）
| A． | -0.064的立方根是0.4 | B． | -9的平方根是±3 | ||
| C． | 0.001的立方根是0.000001 | D． | 16的立方根是$\root{3}{16}$ |
如图所示，正方形网格中每一个小正方形的边长都是1，则每个小格的顶点叫做格点．请以图中的格点为顶点画一个三角形，使三角形的三边长分别为$\sqrt{10}$、$\sqrt{29}$、$\sqrt{37}$．
12．下列计算错误的是（ ）
| A． | $\sqrt{（-4）^{2}}$=4 | B． | $\root{3}{（-6）^{3}}$=-6 | C． | $\sqrt{（196）^{2}}$=196 | D． | （-$\sqrt{9}$）2=-9 |
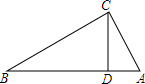如图，在△ABC中，CD⊥AB于D，AD=9，BD=16，CD=12．