题目内容
19.关于x的一元二次方程mx2+(2m-1)x-2=0的根的判别式等于4,则m的值是( )| A. | $\frac{1}{2}$ | B. | $-\frac{3}{2}$ | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$或$-\frac{3}{2}$ |
分析 根据一元二次方程的定义以及根的判别式△=b2-4ac的意义,得出m≠0,且4m2+4m+1=4,把相应的数代入进行计算,即可求出m的值.
解答 解:∵△=(2m-1)2-4×m×(-2)=4m2+4m+1,
∴由题意得:m≠0,且4m2+4m+1=4,
∴m≠0,且(2m+1)2=4,
解得:m1=$\frac{1}{2}$,m2=-$\frac{3}{2}$.
故选D.
点评 本题主要考查一元二次方程根的判别式,掌握根的判别式△=b2-4ac和找出a,b,c的值是本题的关键.也考查了一元二次方程的定义.

练习册系列答案
相关题目
12.下列计算错误的是( )
| A. | $\sqrt{(-4)^{2}}$=4 | B. | $\root{3}{(-6)^{3}}$=-6 | C. | $\sqrt{(196)^{2}}$=196 | D. | (-$\sqrt{9}$)2=-9 |
14.下列二次根式中,属于最简二次根式的是( )
| A. | $\sqrt{{x^2}+2}$ | B. | $\sqrt{12}$ | C. | $\sqrt{\frac{3}{2}}$ | D. | $\sqrt{4{a^3}{b^2}}$ |
8.若将分式$\frac{2x}{x-y}$的分子、分母中的字母的系数都扩大10倍,则分式的值( )
| A. | 扩大10倍 | B. | 扩大10倍 | C. | 不变 | D. | 缩小10倍 |
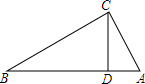 如图,在△ABC中,CD⊥AB于D,AD=9,BD=16,CD=12.
如图,在△ABC中,CD⊥AB于D,AD=9,BD=16,CD=12. 如图,在△ABC中,AI和CI分别平分∠BAC和∠BCA,如果∠B=58°,那么∠AIC=119°.
如图,在△ABC中,AI和CI分别平分∠BAC和∠BCA,如果∠B=58°,那么∠AIC=119°. 张大爷要围成一个矩形花圃.花圃的一边利用足够长的墙另三边用总长为32米的篱笆恰好围成.围成的花圃是如图所示的矩形ABCD.设AB边的长为x米.矩形ABCD的面积为S平方米.
张大爷要围成一个矩形花圃.花圃的一边利用足够长的墙另三边用总长为32米的篱笆恰好围成.围成的花圃是如图所示的矩形ABCD.设AB边的长为x米.矩形ABCD的面积为S平方米.