题目内容
17. 如图,△ABC中,AB=AC,点D,E在BC边上,当BD=CE时,△ABD≌△ACE.(添加一个适当的条件即可)
如图,△ABC中,AB=AC,点D,E在BC边上,当BD=CE时,△ABD≌△ACE.(添加一个适当的条件即可)
分析 根据等边对等角得出∠B=∠C,根据全等三角形的判定推出即可.
解答 解:BD=CE,
理由是:∵AB=AC,
∴∠B=∠C,
在△ABD和△ACE中
$\left\{\begin{array}{l}{AB=AC}\\{∠B=∠C}\\{BD=CE}\end{array}\right.$
∴△ABD≌△ACE(SAS),
故答案为:BD=CE.
点评 本题考查了等腰三角形的性质,全等三角形的判定的应用,此题是一道开放型的题目,答案不唯一,只要填上一个符合的即可.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
8.如果关于x的方程x2-x+m=0有实数根,那么m的取值范围是( )
| A. | m>$\frac{1}{4}$ | B. | m≥$\frac{1}{4}$ | C. | m<$\frac{1}{4}$ | D. | m≤$\frac{1}{4}$ |
5.下列事件中,是确定事件的是( )
| A. | 上海明天会下雨 | B. | 将要过马路时恰好遇到红灯 | ||
| C. | 有人把石头孵成了小鸭 | D. | 冬天,盆里的水结成了冰 |
9.边长为a的正六边形的面积为( )
| A. | $\frac{3\sqrt{3}}{2}$a2 | B. | 6a2 | C. | $\frac{\sqrt{3}}{4}$a2 | D. | 3$\sqrt{3}$a2 |
7.若关于x的方程x2+2mx+m2+3m-2=0有两个实数根x1、x2,则x1(x2+x1)+x22的最小值为( )
| A. | 1 | B. | 2 | C. | $\frac{3}{4}$ | D. | $\frac{5}{4}$ |
 如图,等腰△ABC内接于半径为5的⊙O,AB=AC,tan∠ABC=$\frac{1}{3}$.求BC的长.
如图,等腰△ABC内接于半径为5的⊙O,AB=AC,tan∠ABC=$\frac{1}{3}$.求BC的长.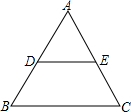 如图,等边△ABC中,点D、E分别为边AB、AC的中点,则∠DEC的度数为120°.
如图,等边△ABC中,点D、E分别为边AB、AC的中点,则∠DEC的度数为120°. 已知:如图,在△ABC中,AB=AC,D为边BC上一点,将线段AB平移至DE,连接AE、AD、EC.
已知:如图,在△ABC中,AB=AC,D为边BC上一点,将线段AB平移至DE,连接AE、AD、EC.