题目内容
16.函数y=$\frac{x+1}{4-2x}$的定义域是x≠2.分析 根据分式有意义的条件是分母不为0;分析原函数式可得关系式4-2x≠0,解可得自变量x的取值范围.
解答 解:根据题意,有4-2x≠0,
解可得x≠2;
故函数y=$\frac{x+1}{4-2x}$的定义域是x≠2.
故答案为x≠2.
点评 本题考查了函数自变量的取值范围,一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数为非负数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.数据6,7,7,6,13,5,6,8的众数是( )
| A. | 5 | B. | 6 | C. | 7 | D. | 5或6或7 |
8.如果关于x的方程x2-x+m=0有实数根,那么m的取值范围是( )
| A. | m>$\frac{1}{4}$ | B. | m≥$\frac{1}{4}$ | C. | m<$\frac{1}{4}$ | D. | m≤$\frac{1}{4}$ |
5.下列事件中,是确定事件的是( )
| A. | 上海明天会下雨 | B. | 将要过马路时恰好遇到红灯 | ||
| C. | 有人把石头孵成了小鸭 | D. | 冬天,盆里的水结成了冰 |
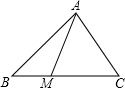 如图,在△ABC中,点M在边BC上,MC=2BM,设向量$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AM}$=$\overrightarrow{b}$,那么向量$\overrightarrow{BC}$=3$\overrightarrow{b}$-3$\overrightarrow{a}$(结果用$\overrightarrow{a}$、$\overrightarrow{b}$表示).
如图,在△ABC中,点M在边BC上,MC=2BM,设向量$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AM}$=$\overrightarrow{b}$,那么向量$\overrightarrow{BC}$=3$\overrightarrow{b}$-3$\overrightarrow{a}$(结果用$\overrightarrow{a}$、$\overrightarrow{b}$表示). 已知:如图,在△ABC中,AB=AC,D为边BC上一点,将线段AB平移至DE,连接AE、AD、EC.
已知:如图,在△ABC中,AB=AC,D为边BC上一点,将线段AB平移至DE,连接AE、AD、EC.