题目内容
 九年级(1)班为即将到来的“五•一”国际劳动节排练节目时需要3个底面圆半径为10厘米,母线长为20厘米的圆锥形小红帽(不计接缝损失).
九年级(1)班为即将到来的“五•一”国际劳动节排练节目时需要3个底面圆半径为10厘米,母线长为20厘米的圆锥形小红帽(不计接缝损失).(1)试确定这种圆锥形小红帽侧面展开图(扇形)的圆心角的度数;
(2)现有宽为40厘米的矩形布料可供选用,按照题目要求在图1中画出使布料能充分利用(最省料)的示意图,并求出矩形布料的长至少为多少厘米.
考点:圆锥的计算,勾股定理,相切两圆的性质
专题:
分析:(1)利用圆锥底面圆的周长等于展开图的扇形弧长求出圆心角即可;
(2)利用扇形的圆心角为180°,圆锥母线长为20厘米,所以这个扇形的半径为20厘米的半圆,结合⊙O1,⊙O2,⊙O3两两外切,由两圆外切的性质得出和勾股定理求出O3E的长,进而得出EO3=O1D,以及矩形布料的长至少应为(20+20
)厘米.
(2)利用扇形的圆心角为180°,圆锥母线长为20厘米,所以这个扇形的半径为20厘米的半圆,结合⊙O1,⊙O2,⊙O3两两外切,由两圆外切的性质得出和勾股定理求出O3E的长,进而得出EO3=O1D,以及矩形布料的长至少应为(20+20
| 3 |
解答: 解:(1)设圆心角的度数为n°,则
解:(1)设圆心角的度数为n°,则
=2π×10.(3分)
所以n=180.所以此圆锥形小红帽侧面展开图的圆心角度数为180°.(5分)
(2)因为扇形的圆心角为180°,圆锥母线长为20厘米,所以这个扇形的半径为20厘米的半圆.
如图1所示,当三个半圆所在圆两两外切,且半圆的直径与长方形的边垂直时,能使布料得以充分利用.(10分)
如图2,连接O1O2,O2O3,O3O1.
因为⊙O1,⊙O2,⊙O3两两外切,AO1=BO2=CO3=20,
所以O1O2=O2O3=O3O1=O1A+CO3=40.
过点O3作O3E⊥O1O2,垂足为E.
因为O2O3=O1O3,
所以O1E=O2E=
O1O2=20.
在△O1EO3中,∠O1EO3=90°,
根据勾股定理EO3=
=
=20
.(15分)
因为四边形ABCD是矩形,
所以AD∥BC,AD=BC,∠A=∠D=90°.
因为AO1=BO2,AO1∥BO2,
所以四边形ABO2O1是矩形.
所以∠AO1O2=90°.
所以O1E∥DO3.
又因为O1E=DO3,
所以四边形O1EO3D是平行四边形.
所以EO3=O1D.
所以AD=AO1+O1D=20+20
.(20分)
因此矩形布料的长至少应为(20+20
)厘米.
 解:(1)设圆心角的度数为n°,则
解:(1)设圆心角的度数为n°,则| nπ×20 |
| 180 |
所以n=180.所以此圆锥形小红帽侧面展开图的圆心角度数为180°.(5分)
(2)因为扇形的圆心角为180°,圆锥母线长为20厘米,所以这个扇形的半径为20厘米的半圆.
如图1所示,当三个半圆所在圆两两外切,且半圆的直径与长方形的边垂直时,能使布料得以充分利用.(10分)
如图2,连接O1O2,O2O3,O3O1.
因为⊙O1,⊙O2,⊙O3两两外切,AO1=BO2=CO3=20,
所以O1O2=O2O3=O3O1=O1A+CO3=40.
过点O3作O3E⊥O1O2,垂足为E.
因为O2O3=O1O3,
所以O1E=O2E=
| 1 |
| 2 |
在△O1EO3中,∠O1EO3=90°,
根据勾股定理EO3=
| O1O32-O1E2 |
| 402-202 |
| 3 |
因为四边形ABCD是矩形,
所以AD∥BC,AD=BC,∠A=∠D=90°.
因为AO1=BO2,AO1∥BO2,
所以四边形ABO2O1是矩形.
所以∠AO1O2=90°.
所以O1E∥DO3.
又因为O1E=DO3,
所以四边形O1EO3D是平行四边形.
所以EO3=O1D.
所以AD=AO1+O1D=20+20
| 3 |
因此矩形布料的长至少应为(20+20
| 3 |
点评:此题主要考查了圆锥的有关计算以及两圆外切的性质和勾股定理等知识,利用相切两圆性质得出EO3=O1D的长是解题关键.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
 如图,半径为2的⊙O与正方形ABCD相切于点P、Q,弦MN=2,且MN在正方形的对角线BD上,则正方形的边长为
如图,半径为2的⊙O与正方形ABCD相切于点P、Q,弦MN=2,且MN在正方形的对角线BD上,则正方形的边长为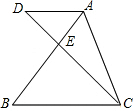 如图,线段AC、BD相交于E,AD∥BC,若AE:EB=1:2,且S△ADE=1,则△EBC的面积等于
如图,线段AC、BD相交于E,AD∥BC,若AE:EB=1:2,且S△ADE=1,则△EBC的面积等于