题目内容
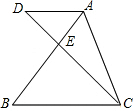如图，线段AC、BD相交于E，AD∥BC，若AE：EB=1：2，且S△ADE=1，则△EBC的面积等于考点：相似三角形的判定与性质
专题：综合题
分析：由AD∥BC，可得△AED∽△BEC，根据相似三角形的性质，由AE：EB=1：2，可得
=
，又S△ADE=1，代入即可求得△EBC的面积；
| S△AED |
| S△BEC |
| AE2 |
| BE2 |
解答：解：如图，
∵AD∥BC，
∴△AED∽△BEC，
∴
=
，
∵AE：EB=1：2，
∴
=
，
又∵S△ADE=1，
∴S△BEC=4；
故答案为：4．
解：如图，∵AD∥BC，
∴△AED∽△BEC，
∴
| S△AED |
| S△BEC |
| AE2 |
| BE2 |
∵AE：EB=1：2，
∴
| S△AED |
| S△BEC |
| 1 |
| 4 |
又∵S△ADE=1，
∴S△BEC=4；
故答案为：4．
点评：本题主要考查了相似三角形的判定与性质，掌握相似三角形的面积比等于相似比的平方．
练习册系列答案
名校课堂系列答案
相关题目
50个同样大小的立方体木块堆砌成如图所示的形状，现在从前、后、左、右和上面五个方向朝这堆木块喷漆，则有
九年级（1）班为即将到来的“五•一”国际劳动节排练节目时需要3个底面圆半径为10厘米，母线长为20厘米的圆锥形小红帽（不计接缝损失）．若m+
与m-
互为相反数，则m的值是（ ）
| 1 |
| 4 |
| 1 |
| 4 |
| A、0 | ||
B、
| ||
C、
| ||
D、
|
已知a（b+2）是一个不为0的常数，且当a=2时，b=1；那么当b=4时，a=（ ）
| A、1 | B、2 | C、3 | D、4 |