题目内容
12. 如图,已知A、B、C是半径为2cm的⊙O上三点,且∠BAC=60°,则扇形OBC的面积为$\frac{4}{3}π$cm2.(结果保留π)
如图,已知A、B、C是半径为2cm的⊙O上三点,且∠BAC=60°,则扇形OBC的面积为$\frac{4}{3}π$cm2.(结果保留π)
分析 根据圆周角定理求出∠BOC的度数,根据扇形的面积公式S=$\frac{nπ{R}^{2}}{360}$计算即可.
解答 解:∠BOC=2∠BAC=120°,
扇形OBC的面积=$\frac{120π×{2}^{2}}{360}$=$\frac{4}{3}π$cm2.
故答案为:$\frac{4}{3}π$cm2.
点评 本题考查的是扇形的面积的计算,掌握扇形的面积公式S=$\frac{nπ{R}^{2}}{360}$是解题的关键.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
2. 如图,点C是线段AB的黄金分割点,则下列各式正确的是( )
如图,点C是线段AB的黄金分割点,则下列各式正确的是( )
 如图,点C是线段AB的黄金分割点,则下列各式正确的是( )
如图,点C是线段AB的黄金分割点,则下列各式正确的是( )| A. | $\frac{AC}{BC}=\frac{AB}{AC}$ | B. | $\frac{BC}{AB}=\frac{AC}{BC}$ | C. | $\frac{AC}{AB}=\frac{AB}{BC}$ | D. | $\frac{BC}{AB}=\frac{AC}{AB}$ |
3.下列代数式中a,-2ab,x+y,x2+y2,-1,单项式共有( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
7.如果A是x的二次多项式,B是x的四次多项式,那么A-B是( )
| A. | 三次多项式 | B. | 二次多项式 | C. | 四次多项式 | D. | 五次多项式 |
4.在3.141、0.33333…、$\sqrt{5}$-$\sqrt{7}$、$\frac{π}{2}$、$±\sqrt{2.25}$、-$\frac{2}{3}$、数0.3030003000003…(相邻两个3之间0的个数逐次增加2)、0这八个数中,无理数的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2. 如图,在△ABC中,AB=AC,∠BAC=80°,AD⊥BC于D,则∠B等于( )
如图,在△ABC中,AB=AC,∠BAC=80°,AD⊥BC于D,则∠B等于( )
 如图,在△ABC中,AB=AC,∠BAC=80°,AD⊥BC于D,则∠B等于( )
如图,在△ABC中,AB=AC,∠BAC=80°,AD⊥BC于D,则∠B等于( )| A. | 70° | B. | 50° | C. | 20° | D. | 40° |
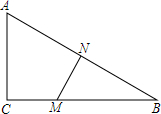 已知△ABC,∠ACB=90°,AC=4,MN垂直平分AB,且BM=2CM,求CM的长.
已知△ABC,∠ACB=90°,AC=4,MN垂直平分AB,且BM=2CM,求CM的长. 如图,已知AB=AC,AB=10cm,CD=3cm,AB的垂直平分线MN交AC于点D,则BD=7cm.
如图,已知AB=AC,AB=10cm,CD=3cm,AB的垂直平分线MN交AC于点D,则BD=7cm.