题目内容
15.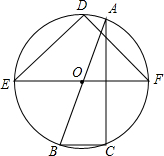 如图,一副三角板ABC和DEF的顶点都在同一个圆上,且EF∥BC,求劣弧DA和劣弧BCF的度数和.
如图,一副三角板ABC和DEF的顶点都在同一个圆上,且EF∥BC,求劣弧DA和劣弧BCF的度数和.
分析 连接OD,根据△DEF是等腰直角三角形可得出OD⊥EF,故∠DOF=90°,再由EF∥BC可知∠AOF=60°,由此可得出∠AOD的度数,进而得出$\widehat{AD}$的度数,根据补角的定义求出∠BOF的度数即可得出$\widehat{BCF}$的度数,由此可得出结论.
解答 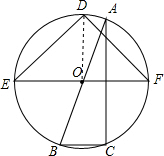 解:连接OD,
解:连接OD,
∵△DEF是等腰直角三角形,
∴OD⊥EF,
∴∠DOF=90°.
∵EF∥BC,
∴∠AOF=60°,
∴∠AOD=90°-60°=30°,
∴$\widehat{AD}$=30°.
∵∠AOF=60°,
∴∠BOF=180°-60°=120°,
∴$\widehat{BCF}$=120°,
∴劣$\widehat{AD}$+劣$\widehat{BCF}$=30°+120°=150°.
点评 本题考查的是圆心角、弧、弦的关系,熟知在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等是解答此题的关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
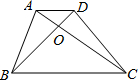 如图所示,在梯形ABCD中,AD∥BC,AD=1,BC=3,△AOD,△AOB,△BOC的面积为S1,S2,S3,那么S1:S2:S3分别等于多少?
如图所示,在梯形ABCD中,AD∥BC,AD=1,BC=3,△AOD,△AOB,△BOC的面积为S1,S2,S3,那么S1:S2:S3分别等于多少?
 如图,已知线段AB,在线段AB上求作点C,使得AC:BC=2:1.(保留作图痕迹).
如图,已知线段AB,在线段AB上求作点C,使得AC:BC=2:1.(保留作图痕迹). 如图,在△ABC中,DE∥AC,EF∥AB,求证:∠EFC+∠FEC+∠DEB=180°.
如图,在△ABC中,DE∥AC,EF∥AB,求证:∠EFC+∠FEC+∠DEB=180°.