题目内容
3.已知$\frac{a}{2}$=$\frac{b}{3}$,$\frac{b}{5}$=$\frac{c}{4}$,求$\frac{a+b}{b-c}$的值.分析 根据比例的性质,可用b表示a,用b表示c,根据分式的性质,可得答案.
解答 解:由$\frac{a}{2}$=$\frac{b}{3}$,$\frac{b}{5}$=$\frac{c}{4}$,得
a=$\frac{2}{3}$b,c=$\frac{4}{5}$b.
$\frac{a+b}{b-c}$=$\frac{\frac{2}{3}b+b}{b-\frac{4}{5}b}$=$\frac{\frac{5}{3}b}{\frac{1}{5}b}$=$\frac{25}{3}$.
点评 本题考查了比例的性质,利用比例的性质得出a=$\frac{2}{3}$b,c=$\frac{4}{5}$b是解题关键.

练习册系列答案
相关题目
13. 如图是某校食堂甲、乙、丙、丁四种午餐受欢迎程度的扇形统计图,则最受欢迎的午餐是( )
如图是某校食堂甲、乙、丙、丁四种午餐受欢迎程度的扇形统计图,则最受欢迎的午餐是( )
 如图是某校食堂甲、乙、丙、丁四种午餐受欢迎程度的扇形统计图,则最受欢迎的午餐是( )
如图是某校食堂甲、乙、丙、丁四种午餐受欢迎程度的扇形统计图,则最受欢迎的午餐是( )| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
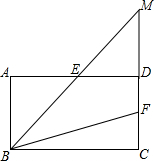 如图,在四边形ABCD中,AB∥CD,AB=CD,∠A=∠ADC,E,F分别为AD,CD的中点,连接BE,BF,延长BE交CD的延长线于点M.
如图,在四边形ABCD中,AB∥CD,AB=CD,∠A=∠ADC,E,F分别为AD,CD的中点,连接BE,BF,延长BE交CD的延长线于点M.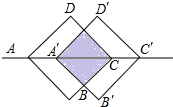 如图所示.正方形ABCD的对角线长为6cm,将此正方形沿对角线AC的方向向右平移2cm得到正方形A′B′C′D′,则平移前后两个图形的重叠部分(阴影部分)的面积为8.
如图所示.正方形ABCD的对角线长为6cm,将此正方形沿对角线AC的方向向右平移2cm得到正方形A′B′C′D′,则平移前后两个图形的重叠部分(阴影部分)的面积为8.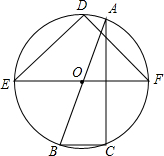 如图,一副三角板ABC和DEF的顶点都在同一个圆上,且EF∥BC,求劣弧DA和劣弧BCF的度数和.
如图,一副三角板ABC和DEF的顶点都在同一个圆上,且EF∥BC,求劣弧DA和劣弧BCF的度数和.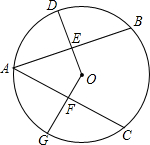 如图,AB=AC,D为$\widehat{AB}$的中点,G为$\widehat{AC}$的中点,求证:DE=GF.
如图,AB=AC,D为$\widehat{AB}$的中点,G为$\widehat{AC}$的中点,求证:DE=GF.