题目内容
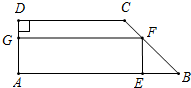 在直角梯形ABCD中,AB∥DC,∠A=90°,AB=6,CD=4,AD=2,作梯形的内接矩形AEFG,使点E在AB上,点F在BC上,点G在AD上.设EF=x.
在直角梯形ABCD中,AB∥DC,∠A=90°,AB=6,CD=4,AD=2,作梯形的内接矩形AEFG,使点E在AB上,点F在BC上,点G在AD上.设EF=x.(1)写出矩形AEFG的面积S与x之间的函数关系解析式,并写出自变量x的取值范围;
(2)写出梯形AGFB的面积S1与x之间的函数解析式.
考点:直角梯形,根据实际问题列二次函数关系式
专题:
分析:(1)过点C作CM⊥AB于M,可以得到四边形AMCD是矩形,△BMC是等腰直角三角形,求出∠B=45°,然后求出EF=BE,再表示出AE,然后根据矩形的面积公式列式即可;
(2)同(1)表示出AE,根据矩形的对边相等可得GF=AE,然后根据梯形的面积公式列式整理即可得解.
(2)同(1)表示出AE,根据矩形的对边相等可得GF=AE,然后根据梯形的面积公式列式整理即可得解.
解答:解:(1)如图,过点C作CM⊥AB于M,
∵AB∥DC,∠A=90°,
∴四边形AMCD是矩形,
∴CM=AD=2,
∴AM=DC=4,
∴BM=AB-AM=6-4=2,
∴CM=BM=2,∠CMB=90°,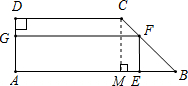
∴△BMC是等腰直角三角形,
∴∠B=45°,
∵EF⊥AB,
∴BE=EF=x,
∴AE=AB-BE=6-x,
∴S=AE×EF=(6-x)x=6x-x2(0<x<2);
(2)由(1)知,∠B=45°,
所以,△BEF是等腰直角三角形,
所以,BE=EF=x,
所以,GF=AE=6-x,
所以,S1=
(6-x+6)•x=-
x2+6x.
∵AB∥DC,∠A=90°,
∴四边形AMCD是矩形,
∴CM=AD=2,
∴AM=DC=4,
∴BM=AB-AM=6-4=2,
∴CM=BM=2,∠CMB=90°,

∴△BMC是等腰直角三角形,
∴∠B=45°,
∵EF⊥AB,
∴BE=EF=x,
∴AE=AB-BE=6-x,
∴S=AE×EF=(6-x)x=6x-x2(0<x<2);
(2)由(1)知,∠B=45°,
所以,△BEF是等腰直角三角形,
所以,BE=EF=x,
所以,GF=AE=6-x,
所以,S1=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了直角梯形,等腰直角三角形的判定与性质,矩形的判定和性质,列二次函数关系式,作辅助线构造出等腰直角三角形和矩形是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 四边形ABCD中,∠BCD=90°,连接AC,∠BAC=90°,∠DAC=45°,BC=6,CD=4,则线段AC的长为
四边形ABCD中,∠BCD=90°,连接AC,∠BAC=90°,∠DAC=45°,BC=6,CD=4,则线段AC的长为 如图,将Rt△ABC纸片沿BD折叠后,C与AB中点E重合,CD=4,则AD=
如图,将Rt△ABC纸片沿BD折叠后,C与AB中点E重合,CD=4,则AD= 如图,将矩形ABCD沿DE折叠,使A点落在BC边上F处,若∠EFB=70°,则∠AED=
如图,将矩形ABCD沿DE折叠,使A点落在BC边上F处,若∠EFB=70°,则∠AED= 如图,等边△ABC中,点D、E、F分别在边BC、CA、AB上,且BD=2DC,CE=2EA,AF=2FB,AD与BE相交于点P,BE与CF相交于点Q,CF与AD相交于点R,则AP:PR:RD=
如图,等边△ABC中,点D、E、F分别在边BC、CA、AB上,且BD=2DC,CE=2EA,AF=2FB,AD与BE相交于点P,BE与CF相交于点Q,CF与AD相交于点R,则AP:PR:RD= 如图,等边△ABC中,点D为BC边的中点,∠BEC=120°,连接AE、DE,求证:AE=2DE.
如图,等边△ABC中,点D为BC边的中点,∠BEC=120°,连接AE、DE,求证:AE=2DE.