题目内容
9．计算题（1）-12013+（$\frac{1}{2}$）-2-（-2）0
（2）（-2x）2•（x2）3÷（-x）2
（3）（x-1）（x-2）-3x（x+3）+2（x+2）（x-1），
（4）先化简，再求代数式（a+2b）（a-2b）+（a+2b）2-4ab的值，其中a=1，b=$\frac{1}{2015}$．
分析 （1）先算乘方，0指数幂与负整数指数幂，再算加减；
（2）先计算积的乘方和幂的乘方，再按照同底数幂的乘除计算；
（3）利用整式的乘法计算，再进一步合并即可；
（4）利用平方差公式和完全平方公式计算，进一步合并代入求得数值即可．
解答 解：（1）原式=-1+4-1
=2；
（2）原式=4x2•（x6）÷x2
=4x6；
（3）原式=x2-3x+2-3x2-9x+2x2+2x-4
=-10x-2；
（4）原式=a2-4b+a2+4ab+4b-4ab
=2a2，
当a=-1时，原式=2．
点评 此题考查整式混合运算与化简求值，掌握计算公式、计算方法，搞清运算顺序是解决问题的关键．
练习册系列答案
全能测控一本好卷系列答案
发散思维新课堂系列答案
相关题目
19．
如图是一块长方形ABCD的场地，长AB=102m，宽AD=51m，从A、B两处入口的中路宽都为1m，两小路汇合处路宽为2m，其余部分种植草坪，则草坪面积为（ ）
如图是一块长方形ABCD的场地，长AB=102m，宽AD=51m，从A、B两处入口的中路宽都为1m，两小路汇合处路宽为2m，其余部分种植草坪，则草坪面积为（ ）| A． | 5050m2 | B． | 5000m2 | C． | 4900m2 | D． | 4998m2 |
14．
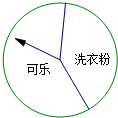某商场“五一”期间为进行有奖销售活动，设立了一个可以自由转动的转盘．商场规定：顾客购物100元以上就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应的奖品．下表是此次活动中的一组统计数据：
（1）完成上述表格；（结果全部精确到0.1）
（2）请估计当n很大时，频率将会接近0.6，假如你去转动该转盘一次，你获得“可乐”的概率约是0.6；（结果全部精确到0.1）
（3）转盘中，表示“洗衣粉”区域的扇形的圆心角约是多少度？
某商场“五一”期间为进行有奖销售活动，设立了一个可以自由转动的转盘．商场规定：顾客购物100元以上就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应的奖品．下表是此次活动中的一组统计数据：| 转动转盘的次数n | 100 | 200 | 400 | 500 | 800 | 1000 |
| 落在“可乐”区域的次数m | 60 | 122 | 240 | 298 | 604 | |
| 落在“可乐”区域的频率$\frac{m}{n}$ | 0.6 | 0.61 | 0.6 | 0.59 | 0.604 |
（2）请估计当n很大时，频率将会接近0.6，假如你去转动该转盘一次，你获得“可乐”的概率约是0.6；（结果全部精确到0.1）
（3）转盘中，表示“洗衣粉”区域的扇形的圆心角约是多少度？
1．在下列性质中，菱形具有而矩形不具有的性质是（ ）
| A． | 内角和等于360° | B． | 对角相等 | ||
| C． | 对角线平分一组对角 | D． | 邻角互补 |
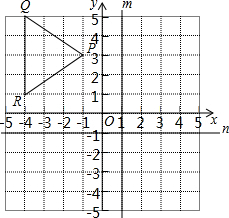已知：△PQR在平面直角坐标系中的位置如图所示：