题目内容
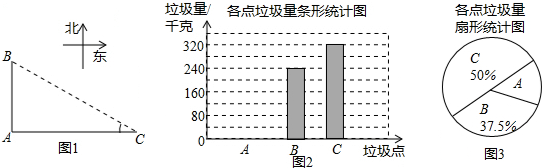
如图1,A,B,C是三个垃圾存放点,点B,C分别位于点A的正北和正东方向,AC=100米.四人分别测得∠C的度数如下表:
他们又调查了各点的垃圾量,并绘制了下列尚不完整的统计图2,图3:
(1)求表中∠C度数的平均数
:
(2)求A处的垃圾量,并将图2补充完整;
(3)用(1)中的
作为∠C的度数,要将A处的垃圾沿道路AB都运到B处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用.(注:sin37°=0.6,cos37°=0.8,tan37°=0.75)
| 甲 | 乙 | 丙 | 丁 | |
| ∠C(单位:度) | 34 | 36 | 38 | 40 |

(1)求表中∠C度数的平均数
. |
| x |
(2)求A处的垃圾量,并将图2补充完整;
(3)用(1)中的
. |
| x |
考点:解直角三角形的应用,扇形统计图,条形统计图,算术平均数
专题:图表型
分析:(1)利用平均数求法进而得出答案;
(2)利用扇形统计图以及条形统计图可得出C处垃圾量以及所占百分比,进而求出垃圾总量,进而得出A处垃圾量;
(3)利用锐角三角函数得出AB的长,进而得出运垃圾所需的费用.
(2)利用扇形统计图以及条形统计图可得出C处垃圾量以及所占百分比,进而求出垃圾总量,进而得出A处垃圾量;
(3)利用锐角三角函数得出AB的长,进而得出运垃圾所需的费用.
解答:解:(1)
=
=37(度);
(2)∵C处垃圾存放量为:320kg,在扇形统计图中所占比例为:50%,
∴垃圾总量为:320÷50%=640(千克),
∴A处垃圾存放量为:(1-50%-37.5%)×640=80(kg),占12.5%.
补全条形图如下:

(3)∵AC=100米,∠C=37°,
∴tan37°=
,
∴AB=ACtan37°=100×0.75=75(米),
∵运送1千克垃圾每米的费用为0.005元,
∴运垃圾所需的费用为:75×80×0.005=30(元),
答:运垃圾所需的费用为30元.
. |
| x |
| 34+36+38+40 |
| 4 |
(2)∵C处垃圾存放量为:320kg,在扇形统计图中所占比例为:50%,
∴垃圾总量为:320÷50%=640(千克),
∴A处垃圾存放量为:(1-50%-37.5%)×640=80(kg),占12.5%.
补全条形图如下:

(3)∵AC=100米,∠C=37°,
∴tan37°=
| AB |
| AC |
∴AB=ACtan37°=100×0.75=75(米),
∵运送1千克垃圾每米的费用为0.005元,
∴运垃圾所需的费用为:75×80×0.005=30(元),
答:运垃圾所需的费用为30元.
点评:此题主要考查了平均数求法以及锐角三角三角函数关系以及条形统计图与扇形统计图的综合应用,利用扇形统计图与条形统计图获取正确信息是解题关键.

练习册系列答案
相关题目
抛物线y=(x-1)2+2与y轴交点坐标为( )
| A、(0,1) |
| B、(0,2) |
| C、(1,2) |
| D、(0,3) |
 在平面内正方形ABCD与正方形CEFH如图放置,连DE,BH,两线交于M.求证:
在平面内正方形ABCD与正方形CEFH如图放置,连DE,BH,两线交于M.求证: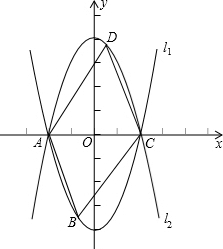 如图,已知抛物线l1:y=x2-4与x轴相交于A,C两点.
如图,已知抛物线l1:y=x2-4与x轴相交于A,C两点.