题目内容
17.(1)已知2a-1的立方根是3,3a+b-1的算术平方根是8,求a+2b的平方根.(2)若一个正数x的平方根是2a-1和-a+2,求这个正数x.
分析 (1)根据立方根与算术平方根的定义得到2a-1=27,3a+b-1=64,则可计算出a=14,b=23,然后计算a+2b后利用平方根的定义求解.
(2)首先根据整数有两个平方根,它们互为相反数可得2a-1-a+2=0,解方程可得a,然后再求出这个正数即可.
解答 解:(1)根据题意得2a-1=27,3a+b-1=64,解得a=14,b=23,
所以a+2b=14+46=60,
而60的平方根为±2$\sqrt{15}$,
所以a+2b的平方根为±2$\sqrt{15}$;
(2)由题意得:2a-1-a+2=0,
解得:a=-1,
2a-1=-3,-a+2=3,
则这个正数为9.
点评 此题主要考查了平方根、立方根、算术平方根,关键是掌握一个正数有两个平方根,这两个平方根互为相反数.

练习册系列答案
相关题目
5.下列从左到右的变形属于因式分解的是( )
| A. | x2-9+6x=(x+3)(x-3)+6x | B. | (x+5)(x-2)=x2+3x-10 | ||
| C. | x2-8x+16=(x-4)2 | D. | -6a2b=-3a﹒2ab |
9.如图①,四边形ABCD中,BC∥AD,∠A=90°,点P从A点出发,沿折线AB→BC→CD运动,到点D时停止,已知△PAD的面积s与点P运动的路程x的函数图象如图②所示,则点P从开始到停止运动的总路程为( )
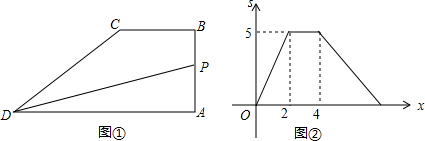

| A. | 4 | B. | 2+$\sqrt{13}$ | C. | 5 | D. | 4+$\sqrt{13}$ |
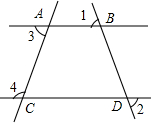 如图,直线AB、CD分别与直线AC相交于点A、C,与直线BD相交于点B、D.若∠1=∠2,∠3=72°,求∠4的度数.
如图,直线AB、CD分别与直线AC相交于点A、C,与直线BD相交于点B、D.若∠1=∠2,∠3=72°,求∠4的度数.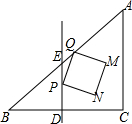 如图,在△ABC中,∠C=90°,AC=BC=12cm,D为BC边中点.DE⊥BC交边AB于点E.点P从点E出发.以1cm/s的速度沿ED向终点D运动.同时点Q从点E出发,以$\sqrt{2}$cm/s的速度沿EA向终点A运动.以PQ为边在∠AED的内部作正方形PQMN.设正方形PQMN与△ABC重叠部分图形的面积为S(cm2).点P的运动时间为t(s).
如图,在△ABC中,∠C=90°,AC=BC=12cm,D为BC边中点.DE⊥BC交边AB于点E.点P从点E出发.以1cm/s的速度沿ED向终点D运动.同时点Q从点E出发,以$\sqrt{2}$cm/s的速度沿EA向终点A运动.以PQ为边在∠AED的内部作正方形PQMN.设正方形PQMN与△ABC重叠部分图形的面积为S(cm2).点P的运动时间为t(s).