题目内容
2.在直角坐标系中,直线y=-$\frac{3}{4}$x+3与x轴和y轴分别交于A、B两点,在y轴上取一点C,如果使B关于直线AC的对称点在x轴上,求点C的坐标.分析 如图,首先求出OA、OB、AB的长度;运用角平分线的性质求出OC的长度,即可解决问题.
解答 解:过C作CD⊥AB于D,如图1,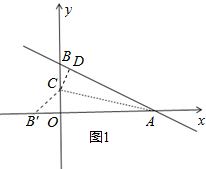
对于直线y=-$\frac{3}{4}$x+3,
当x=0,得y=3;
当y=0,x=4,
∴A(4,0),B(0,3),即OA=4,OB=3,
∴AB=5,
又∵坐标平面沿直线AC折叠,使点B刚好落在x轴上,
∴AC平分∠OAB,
∴CD=CO=n,则BC=3-n,
∴DA=OA=4,
∴DB=5-4=1,
在Rt△BCD中,DC2+BD2=BC2,
∴n2+12=(3-n)2,解得n=$\frac{4}{3}$,
∴点C的坐标为(0,$\frac{4}{3}$);
当点B关于AC的对称点D落在x轴的正半轴时,此时AD=AB=5,
由对称性可得BC=DC,
则OD=AD+OA=5+4=9,
设OC=m,则DC=BC=OB+OC=3+m,
在RT△COD中,有OD2+OC2=DC2,
即有92+m2=(3+m)2,
解得:m=12,
此时C的坐标为(0,-12)
故点C的坐标为(0,$\frac{4}{3}$)或(0,-12).
点评 本题考查了求直线与坐标轴交点的坐标的方法:分别令x=0或y=0,求对应的y或x的值;也考查了折叠的性质和勾股定理.

练习册系列答案
相关题目
14.若3ax2+$\frac{b}{3}$x+4=3x2-x+4对于任何x都成立,则a+b等于( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
11.与原点距离为7的点表示的数是( )
| A. | 7 | B. | -7 | C. | 7和-7 | D. | 0 |
 如图,在宽为20m,长为30m的矩形地块上修建两条同样宽为1m的道路,余下部分作为耕地.根据图中数据计算,耕地的面积为551m2.
如图,在宽为20m,长为30m的矩形地块上修建两条同样宽为1m的道路,余下部分作为耕地.根据图中数据计算,耕地的面积为551m2. 已知,如图所示,在△ABC中,AB>AC,∠ABC的平分线与∠ACB的平分线相交于O点,猜想OB与OC的大小关系.
已知,如图所示,在△ABC中,AB>AC,∠ABC的平分线与∠ACB的平分线相交于O点,猜想OB与OC的大小关系.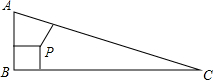 如图,△ABC中,∠B=90°,两直角边AB=7,BC=24,三角形内有一点P到各边的距离相等,则这个距离是( )
如图,△ABC中,∠B=90°,两直角边AB=7,BC=24,三角形内有一点P到各边的距离相等,则这个距离是( )